Contents

Analytisk lösning till ordinär differentialekvation

% u'(t) = u(t), 0 <= t <= 2
% u(0) = 1
% har den allmänna lösningen u(t) = C*exp(t)  (där C är en konstant)
% Villkoret u(0) = 1 ger C = 1. Vi får lösningen u(t) = exp(t);
t = linspace(0,2);
figure(1);clf
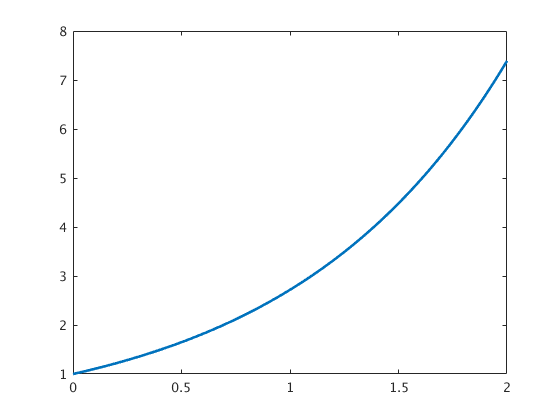
plot(t,exp(t),'linewidth',2);

Olika begynnelsevärden ger olika värden pä konstanten

% u'(t) = u(t), 0 <= t <= 2
% u(0) = 2
hold on
plot(t,2*exp(t),'r');  % u(t) = 2*exp(t)

% u'(t) = u(t), 0 <= t <= 2
% u(0) = 3
plot(t,3*exp(t),'k');  % u(t) = 3*exp(t)
l=legend('$u(t) = e^t$','$u(t) = 2e^t$','$u(t) = 3e^t$','location','NorthWest');
l.FontSize=17;
l.Interpreter='latex';

Eulers metod

clear all
% ODE (allmän formulering):
% u'(t) = f( t,u(t) ),  a <= t <= b
% u(a) = ua

% Eulers metod:
% u(1) = ua
% u(i+1) = u(i) + h*f(t(i),u(i))

% Exemplet ovan igen:
% u'(t) = u(t), 0 <= t <= 2
% u(0) = 1
f = @(t,u)u;
a = 0; b = 2; ua = 1;
N = 4; h = (b-a)/N;
t = a + (0:N)*h;  %alt t = linspace(a,b,N+1);

U(1) = ua;
for i = 1:N
    U(i+1) = U(i) + h*f(t(i),U(i));
end
plot(t,U,'b*')

% Kortare steglängd
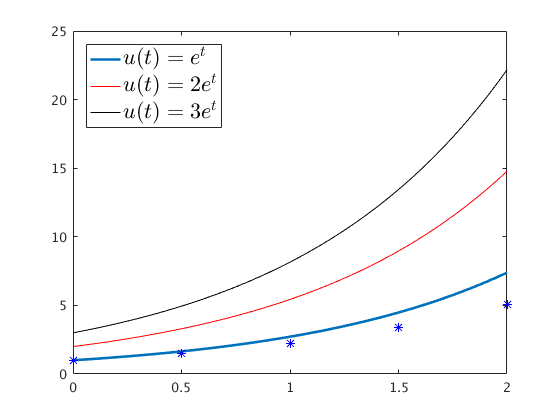
clear U
N = 40; h = (b-a)/N;
t = a + (0:N)*h;  %alt t = linspace(a,b,N+1);

U(1) = ua;
for i = 1:N
    U(i+1) = U(i) + h*f(t(i),U(i));
end
plot(t,U,'-*c')

t=0:0.25:1.75; y=0:1:20;
[T,Y]=meshgrid(t,y);
dT=ones(size(T));
dY=Y;
q=quiver(T,Y,dT,dY,3,'ShowArrowHead', 'off');
axis([0,2,0,25])

Published with MATLAB® R2016b