EXEMPEL 1: Ytor, gradientfält  

Vi betraktar funktionen 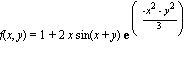   f(x, y) = 1+2*x*sin(x+y)*exp((-x^2-y^2)/3)  

och laddar in på en gång alla nödvändiga paket:

> with(linalg):with(plots):with(plottools):

> f:=(x,y)->1+2*x*sin(x+y)*exp(-(x^2+y^2)/3):        

Beräkning av gradientvektorn och sedan normering  (skriv alltid ut det!):

> v:=grad(f(x,y),[x,y]):vn:=normalize(v):

Nu kan vi rita gradientfältet i xy-planet med fieldplot (gör det först för att kolla att allt funkar). Vi ritar på en gång gradientvektorn tillsammans med nivåkurvorna vilkas antal väljes med "contours = n ", default är n= 10). Glöm ej  axis=constrained  (kan du göra med musen förstås) för att se att de är ortogonala.  

> p1:=fieldplot(vn,x=-3..3,y=-2.6..2.3,arrows=SLIM,color=red):

> p2:=contourplot(f(x,y),x=-3..3,y=-2.6..2.3,contours=22,color=blue,numpoints=999):

> display([p1,p2],scaling=constrained);

[Plot]

Men helst vill vi ju se funktionsytan. Den ritas med plot3d, kanske med nivåkurvorna i ytan (det klickar vi fram med musen: klicka med högermusen i figuren och välj style = patch and contour, gör det nu på en gång för att kolla; pröva även de andra inställningarna, bl.a. de olika  color = light schema...), men allrahelst förstås vill vi se allt: för att kunna rita en 2d-plot och en 3d-plot tillsammans med display, "transformerar" vi 2d-plotten så att den ligger i rummet med z-koordinaten t.ex. z = -0.3 så att definitionsmängden med nivåkurvorna ligger synligt under ytan, vidare  kan vi fylla ut definitionsområdet med  filled=true; med labels= ... får vi maple att skriva ut namn på axlarna (du kan välja vilka):

> p2ny:=contourplot(f(x,y),x=-3..3,y=-2.6..2.3,coloring=[yellow,red],filled=true):

> pr:=transform((x,y)->[x,y,-0.3]):

> pxy:=pr(p2ny):

> p3:=plot3d(f(x,y),x=-3.1..3.1,y=-2.6..2.3):

> display([p3,pxy],labels=[x,y,z]);

[Plot]

Definitionsområdet kan vara en mängd som begränsas av kurvor. Låt oss t.ex. rita vår yta ovanför en cirkelskiva. Dra ytan med musen så att du ser den från alla håll:

> p4:=plot3d(f(x,y),x=-3..3,y=-sqrt(9-x^2)..sqrt(9-x^2),grid=[30,31]):

> pdef:=plot3d(0,x=-3..3,y=-sqrt(9-x^2)..sqrt(9-x^2),style=patchnogrid,color=yellow):

> display([p4,pdef]);

[Plot]

Tangentplanet i en punkt  (a,b)  har ekvationen

> tangplan:=(x,y)->f(a,b)+D[1](f)(a,b)*(x-a)+D[2](f)(a,b)*(y-b);

tangplan := proc (x, y) options operator, arrow; f(a, b)+D[1](f)(a, b)*(x-a)+D[2](f)(a, b)*(y-b) end proc

Du kan naturligtvis utnyttja vektorn  v  ovan, men med skalärprodukten räknar vi först nedan (ex2). I punkten (-1,0) t.ex. har vi

> a:=-1:b:=0:expand(tangplan(x,y));

1+4/3*sin(1)*exp((-1)/3)-2/3*sin(1)*exp((-1)/3)*x-2*cos(1)*exp((-1)/3)*x-2*cos(1)*exp((-1)/3)-2*cos(1)*exp((-1)/3)*y

Vi ritar ytan och tangentplan i samma plot med display (eller display3d), det har fördelen att vi kan välja färg och områden separat:

> ptan:=plot3d(tangplan(x,y),x=-1.5..0,y=-1..1,grid=[40,40],color=cyan,style=patchnogrid):

> pyta:=plot3d(f(x,y),x=-3..3,y=-sqrt(9-x^2)..sqrt(9-x^2)):

> display([pyta,ptan]);

[Plot]

Du kan också skriva in ytorna som mängd. För att inte tangentplanet skall dominera kan du då bestämma hur mycket som skall ritas med view:

> plot3d({f(x,y),tangplan(x,y)},x=-3..3,y=-sqrt(9-x^2)..sqrt(9-x^2),view=[-3..3,-2..3,0.5..2.6],grid=[39,39]): kolla! Vrid tills du är nöjd!

Till sist: antalet nivåkurvor kan du ange även i vanlig 3d-plot (och välja efteråt med musen hur du vill plotta ytan):

> plot3d(f(x,y),x=-3..3,y=-sqrt(9-x^2)..sqrt(9-x^2),contours=25,grid=[44,45],title=`nivåkurvor`);

[Plot]

EXEMPEL2: kurvor, arbete, längd

Vi betraktar den koniska skruvlinjen

> u:=t->[2^(1/2)*t*cos(t),2^(1/2)*t*sin(t),2*t];

u := proc (t) options operator, arrow; [2^(1/2)*t*cos(t), 2^(1/2)*t*sin(t), 2*t] end proc

och sträckan

> l:=t->[t,t,2*t]:

Du kan rita dem med

> spacecurve({u(t),l(t)},t=0..33*Pi/4,numpoints=789):

eller med display och olika färger:

> p10:=spacecurve(u(t),t=0..33*Pi/4,numpoints=999,color=blue):

> p11:=spacecurve(l(t),t=0..33*Pi/4,color=red,thickness=2):

> display([p10,p11],labels=[x,y,z]);

[Plot]

Ändå bättre ser du skruvlinjen, om du ritar en slang omkring den, här med radie r = 1.2:

> tubeplot(u(t),t=0..33*Pi/4,radius=1.2,numpoints=565,scaling=constrained):

Som alltid: titta!! Vrid och begrunda, vilken fin spiral det t.ex. blir sett rakt uppifrån!

Allrabäst ser du det kanske om du ritar konen också:

> p12:=plot3d(2*sqrt(1/2*x^2+1/2*y^2),x=-36..36,y=-sqrt(1296-x^2)..sqrt(1296-x^2),grid=[33,33],style=patchnogrid,color=[1,1,1+x]):

> display([p10,p12,p11]);

[Plot]

Nu till arbetet: vi betraktar kraftfältet

> F:=(x,y,z)->[cos(x+y+z),(x^2+y^2+z^2)*exp(-z/10),sin(z)+x*y]:

Det arbete som  F  uträttar då en partikel förflyttas längs skruvlinjen, resp. längs sträckan fås nu sä här (skalärprodukt: se labben till delA):

> tangvektskruv:=diff(u(t),t);tangvektlin:=diff(l(t),t);

tangvektskruv := [2^(1/2)*cos(t)-2^(1/2)*t*sin(t), 2^(1/2)*sin(t)+2^(1/2)*t*cos(t), 2]

tangvektlin := [1, 1, 2]

> arbskruv:=int(dotprod(F(u(t)[1],u(t)[2],u(t)[3]),tangvektskruv,orthogonal),t=0..33*Pi/4):

> evalf(%);

591.7285439

> arblin:=int(dotprod(F(l(t)[1],l(t)[2],l(t)[3]),tangvektlin,orthogonal),t=0..33*Pi/4):

> evalf(%);

12942.98502

Anmärkning: är F  konservativt?

Till sist beräknar vi längden av vår koniska skruvlinje:

> tv:=tangvektskruv:ds:=sqrt(sum(tv[k]^2,k=1..3));

ds := (4+(2^(1/2)*cos(t)-2^(1/2)*t*sin(t))^2+(2^(1/2)*sin(t)+2^(1/2)*t*cos(t))^2)^(1/2)

> langd:=evalf(int(ds,t=0..33*Pi/4));

langd := 483.2706976

EXEMPEL 3: Taylorutveckling

Vi betraktar funktionen

> g := proc (x) options operator, arrow; 16/sqrt(4+sin(2*x)^3*cos(x)-sin(x)) end proc

> plot(g(x),x=-2..8,title=`kurvan y=g(x)`);

[Plot]

Maclaurinpolynomet av grad  n  till  g  fås med  

> tp:=n->convert(taylor(g(x),x=0,n+1),polynom):

Titta t.ex. på  P[3]  och  P[6] :

> tp(3);tp(6);

8+x+3/16*x^2-3121/384*x^3

8+x+3/16*x^2-3121/384*x^3-12509/4096*x^4+9365041/491520*x^5+51720067/2621440*x^6

Nu ritar vi  g  och några Maclaurinpolynom till  g, antingen som en mängd funktioner (som då får olika färgar), eller med display, då kan man välja färg och tjocklek för varje kurva separat. Rita först  g  för att få bra intervall för  x  resp.  y:

> plot({g(x),tp(3),tp(6),tp(10),tp(48),tp(81)},x=-0.6..0.6,y=7.8..8.2);

[Plot]

Eller med  display:

> p:=plot(g(x),x=-0.6..0.6,y=7.8..8.2,color=black,thickness=2,numpoints=1234):

> pol:=n->plot(tp(n),x=-0.6..0.6,y=7.8..8.2):

> display([p,pol(4),pol(9),pol(15),pol(27)]): (plotta det!)

Vill du få olika färger kan du göra det smart, läs  ?plot/color, eller du definierar färgen för varje kurva (går ju snabbt att kopiera med musen). Du kan sedan rita det animerat, se nedan!

> p1:=plot(tp(4),x=-0.6..0.6,y=7.8..8.2,color=green):
p2:=plot(tp(9),x=-0.6..0.6,y=7.8..8.2,color=blue):
p3:=plot(tp(15),x=-0.6..0.6,y=7.8..8.2,color=magenta):
p4:=plot(tp(27),x=-0.6..0.6,y=7.8..8.2,color=red):

> display([p,p1,p2,p3,p4]);

[Plot]

Till sist beräknar och ritar vi Taylorpolynomet till  f(x, y)  från ex.1:

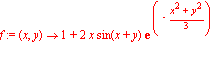
> f := proc (x, y) options operator, arrow; 1+2*x*sin(x+y)*exp(-(x^2+y^2)/3) end proc

> mcl:=mtaylor(f(x,y),[x,y]);

mcl := 1+2*x^2+2*y*x-x^4-5/3*y*x^3-5/3*y^2*x^2-y^3*x

> pmt:=plot3d(mcl,x=-1..1,y=-sqrt(1-x^2)..sqrt(1-x^2),color=red):
pyta:=plot3d(f(x,y),x=-1..1,y=-sqrt(1-x^2)..sqrt(1-x^2),color=green):
pdef2:=plot3d(0,x=-1..1,y=-sqrt(1-x^2)..sqrt(1-x^2),style=patchnogrid):
display3d([pmt,pyta,pdef2],grid=[43,45],title=`ganska bra, va? Vrid och beundra`);

[Plot]

Animation av taylorapproximationen

Just för approximationer är det väldigt givande att utnyttja programmens möjligheter till "animerad framställning". I maple går det med  insequence = true (läs även om  animate).

Vi tar ett enkelt exempel:

> ff:=x->sin(x)+cos(x):

> display(seq(plot([convert(taylor(ff(x),x=0,3*i),polynom),ff(x)],x=-14..14,y=-2..2,axes=frame,tickmarks=[2,2]),i=1..12),insequence=true);

[Plot]

Klicka på figuren, då kan du spela upp det (välj lägre hastighet, eller gå framåt stegvis...), det är väldigt instruktivt, gör det!!
Du kan även printa ut alla "frames":

> display(%);

[Plot]

LYCKA TILL

Bernhard