För att invertera ![]() bestämmer vi en största gemensam delare
till p(x) och x+1 med Euklides algoritm:
bestämmer vi en största gemensam delare
till p(x) och x+1 med Euklides algoritm:
p(x)=(x+1)(x+1)-2
Isvar: ![]()
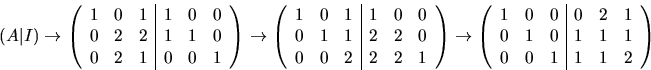
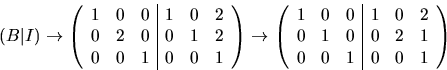
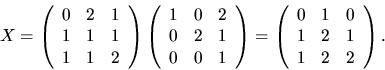
svar: 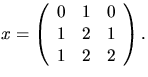
Eftersom ![]() och
och ![]() har
vi
har
vi
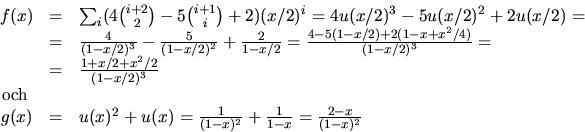
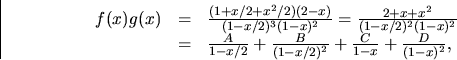
![]()
![]()
svar:
![]() .
.
![]()
![]()
![]()
svar: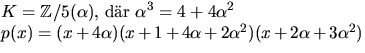
Vi undersöker om f(x)=1+3x+4x2+2x3+x4 faktoriserar och ser att f(2)=0, så f(x)=(x+3)(x3+4x2+2x+2). Men även för g(x)=x3+4x2+2x+2 gäller g(2)=0, så f(x)=(x+3)2(x2+x+4)=(x+3)2(x+3)2=(x+3)4.
De polynom i Z/5[x]/(x+3)4 som är inverterbara är
de som inte delas av x+3. Antalet som delas av x+3 är 53.
Antalet element i gruppen ![]() är
alltså
är
alltså ![]() . Enligt Lagranges sats delar
ordningen av x talet 500, dvs ordningen är
. Enligt Lagranges sats delar
ordningen av x talet 500, dvs ordningen är
![]() eller 500.
Den är uppenbarligen varken 1 eller 2.
eller 500.
Den är uppenbarligen varken 1 eller 2.
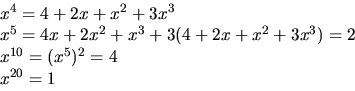
svar: 20.