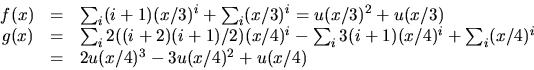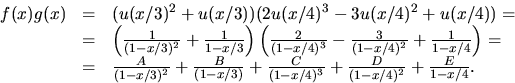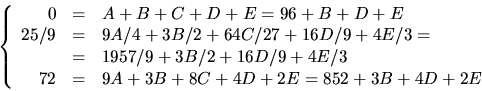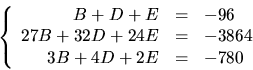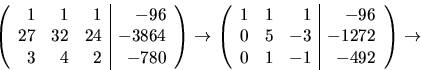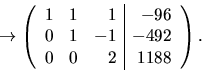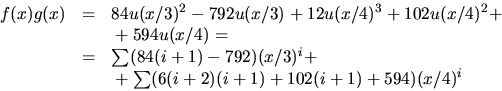Lösningar till tentamen i Aritmetik och algebra, del
2, 98 xx 02.
- 4.
- Det gäller att visa att
![$p(x)=x^{3}+2x+4\in \mathbb Z/5[x]$](img1.gif) är
irreducibelt. Etftersom polynomt är av grad 3 räcker det, enligt
faktorsatsen, att kontrollera att det saknar nollställe i
är
irreducibelt. Etftersom polynomt är av grad 3 räcker det, enligt
faktorsatsen, att kontrollera att det saknar nollställe i 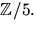 Vi har
Vi har
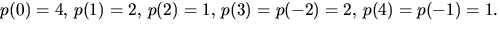
Därmed är 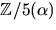 en kropp.
en kropp.
Vi bestämmer inversen med Euklides algoritm för en största gemensam
delare till polynomen 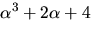 och
och
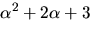 och får
och får
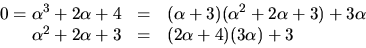
Baklänges ger detta:
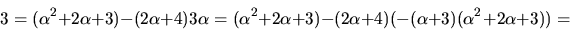
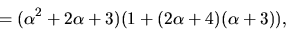
så
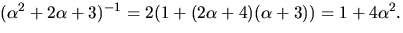
svar: 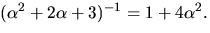
- 5.
- Överför A på trappstegsform med radoperationer:
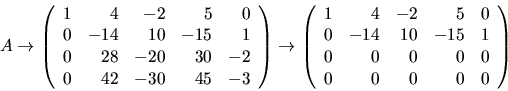
Detta ger
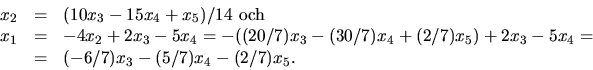
Allmänna lösningen är alltså
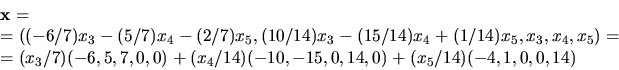
Vi ser att vektorerna 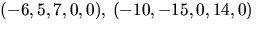 och
(-2,1,0,0,14) genererar lösningsrummet. Det är linjärt oberoende ty
den allmänna lösningen är nollvektorn bara om x3=x4=x5=0.
och
(-2,1,0,0,14) genererar lösningsrummet. Det är linjärt oberoende ty
den allmänna lösningen är nollvektorn bara om x3=x4=x5=0.
svar: 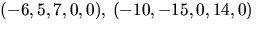 och (-4,1,0,0,14).
och (-4,1,0,0,14).
- 6.
- Det karaktäristiska polynomet är x2-2x-3=(x+1)(x-3). Den allmänna
lösningen till rekursionsekvationen an=4an-1-3an-2 är
därför
an=A(1)n+B3n.
Konstanterna A och B ska bestämmas så att 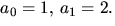 Detta ger ekvationssystemet
Detta ger ekvationssystemet
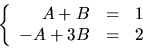
med lösningen B=3/4 och A=1/4. Detta ger
an=(1+3n+1)/4.
svar: an=((-1)n+3n+1)/4.
- 7.
- Eftersom polynomet
![$x^{2}+3x-1\in \mathbb Q[x]$](img18.gif) är av grad 2 är det irreducibelt
om det saknar faktor av grad 1, dvs rationellt nollställe enligt
Faktorsatsen. Dem möjliga rationella nollstöllena ör
är av grad 2 är det irreducibelt
om det saknar faktor av grad 1, dvs rationellt nollställe enligt
Faktorsatsen. Dem möjliga rationella nollstöllena ör 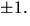 Inget duger.
Inget duger.
Vi har därför kroppen 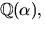 där
där 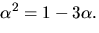 Polynomet x2+3x-1 faktoriserar (enligt Faktorsatsen) som
Polynomet x2+3x-1 faktoriserar (enligt Faktorsatsen) som 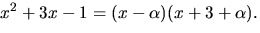 Vi undersöker om x2+3 har något nollställe i
Vi undersöker om x2+3 har något nollställe i 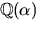 genom att sätta
genom att sätta 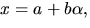 där
där 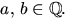 Vi ska försöka
lösa ekvationen
Vi ska försöka
lösa ekvationen 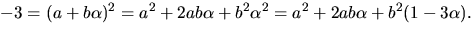 Detta ger ekvationssystemet
Detta ger ekvationssystemet
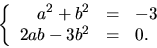
Vi ser att första ekvationen saknar lösning, så x2+3 saknar
nollställe i 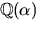 och är därför irreducibelt i
och är därför irreducibelt i ![$\mathbb
Q(\alpha)[x],$](img28.gif) eftersom det är av grad 2.
eftersom det är av grad 2.
Vi får en kropp 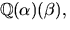 där
där 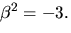 Polynbomet x2+3 faktoriserar (enligt Faktorsatsen) som
Polynbomet x2+3 faktoriserar (enligt Faktorsatsen) som 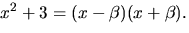
svar: 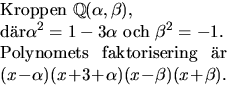
- 8.
- Sätt
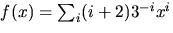 och
och
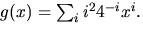 Den sökta summan är koefficienten
framför xn i f(x)g(x).
Den sökta summan är koefficienten
framför xn i f(x)g(x).
Vi uttrycker först f(x) och g(x) med hjälp av
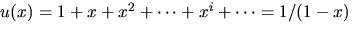 och använder att
och använder att
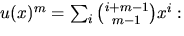
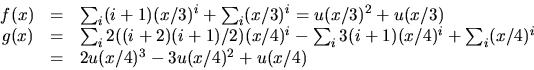
Vi beräknar f(x)g(x) genom partialbråksuppdelning:
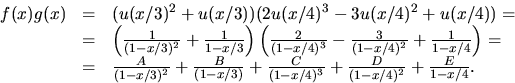
Konstanterna A och C kan bestämmas med handpåläggning och man får
(x=3 resp x=4) 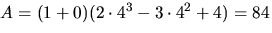 och
C=((-3)2-3)(2+0+0)=12. Sätter vi
och
C=((-3)2-3)(2+0+0)=12. Sätter vi 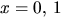 respektive 2
får vi ekvationssystemet
respektive 2
får vi ekvationssystemet
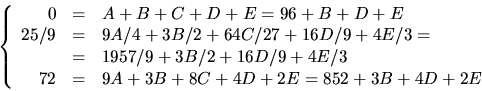
Förenkling ger
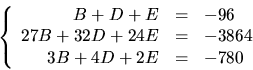
Radoperationer på den utökade koefficientmatrisen ger
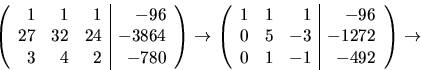
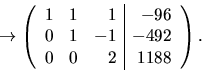
Detta ger 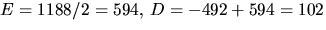 och B=-96-102-594=-792 och
därför
och B=-96-102-594=-792 och
därför
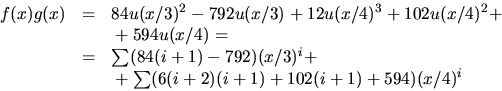
Koefficienten framför xn i f(x)g(x) är därför
(84n-708)3-n+(6n2+120i+708)4-n.
svar: Summan är (84n-708)3-n+(6n2+120n+708)4-n
![]() en kropp.
en kropp.
![]() och
och
![]() och får
och får
![]()
![]()
![]()
![]()
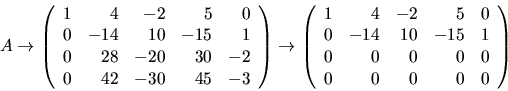
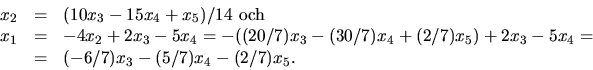
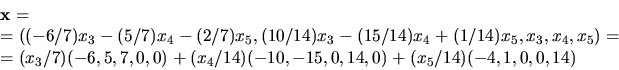
![]() och (-4,1,0,0,14).
och (-4,1,0,0,14).
![]()
![]() där
där ![]() Polynomet x2+3x-1 faktoriserar (enligt Faktorsatsen) som
Polynomet x2+3x-1 faktoriserar (enligt Faktorsatsen) som ![]() Vi undersöker om x2+3 har något nollställe i
Vi undersöker om x2+3 har något nollställe i ![]() genom att sätta
genom att sätta ![]() där
där ![]() Vi ska försöka
lösa ekvationen
Vi ska försöka
lösa ekvationen ![]() Detta ger ekvationssystemet
Detta ger ekvationssystemet
![]()
![]() där
där ![]() Polynbomet x2+3 faktoriserar (enligt Faktorsatsen) som
Polynbomet x2+3 faktoriserar (enligt Faktorsatsen) som ![]()
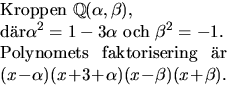
![]() och använder att
och använder att
![]()