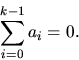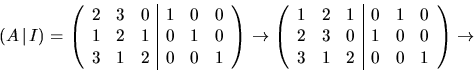

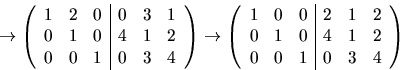
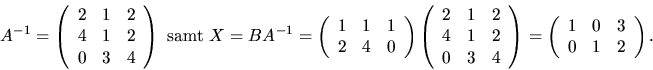
Svar: 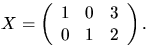
![]()
![]()
Svar: ![]() .
.
En faktor av grad 1 motsvarar ett nollställe i ![]() enligt
faktorsatsen. Vi har
enligt
faktorsatsen. Vi har ![]() och p(2)=p(-1)=2, så
polynomet saknar faktor av grad 1 i
och p(2)=p(-1)=2, så
polynomet saknar faktor av grad 1 i ![]() .
.
För att undersöka eventuell faktor av grad 2 ansätter vi
p(x)=(x2+ax+b)(x2+cx+d), där ![]() och d är i
och d är i
![]() . Identifiering av koefficienter ger ekvationssystemet
. Identifiering av koefficienter ger ekvationssystemet
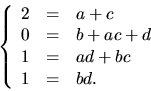
Polynomet p(x) är alltså irreducibelt i ![]() och
därmed är
och
därmed är ![]() där
där
![]() en kropp.
Polynomet p(x) har nollstället
en kropp.
Polynomet p(x) har nollstället ![]() och eftersom
p(x)3=p(x3) kommer även
och eftersom
p(x)3=p(x3) kommer även ![]() och
och
![]() . Eftersom ett polynom inte kan ha fler nollställen
i en kropp än sin grad är dessa samtliga (om de är olika). Vi har
. Eftersom ett polynom inte kan ha fler nollställen
i en kropp än sin grad är dessa samtliga (om de är olika). Vi har
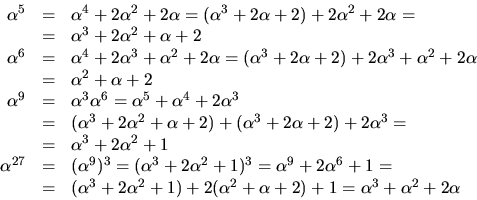
![]()
Svar: Om ![]() där
där
![]() är
är
![]() i K[x].
i K[x].
![]()
![]()
Om vi multiplicerar f(x) med (1-x)-1 får vi en formell
potensserie vars koefficient framför xn är
![]() . Den sökta summan är alltså koefficienten
framför xn i f(x)/(1-x). Partialbråksuppdenling ger
. Den sökta summan är alltså koefficienten
framför xn i f(x)/(1-x). Partialbråksuppdenling ger
![]()
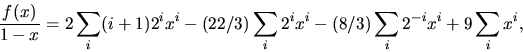
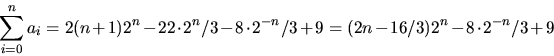
Svar: ![]() .
.
![]()
![]()
Koefficienten framför xk-1 i vänstra ledet är den sökta summan
![]() medan den är i högra ledet. Vi har alltså
visat att
medan den är i högra ledet. Vi har alltså
visat att