Tentamen i MAN011 Aritmetik och algebra, del 2, 98 01 17.
- 1.
- Formulera och bevisa faktorsatsen för polynom i K[x], där K
är en kropp.
- 2.
- (a)
- Vad menas med att ett polynom i K[x], där K är en kropp,
är irreducibelt?
- (b)
- Visa att varje polynom av grad
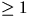 i K[x] kan
skrivas som en produkt av irreducibla polynom.
i K[x] kan
skrivas som en produkt av irreducibla polynom.
- 3.
- Formulera och bevisa Eisensteins kriterium.
- 4.
- Visa att
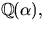 där
där 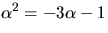 är en kropp
och bestäm inversen till
är en kropp
och bestäm inversen till 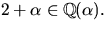
- 5.
- Matrisen
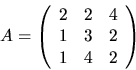
har element i 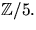 Bestäm matriser C och D så att
A=CDC-1 och D är diagonal.
Bestäm matriser C och D så att
A=CDC-1 och D är diagonal.
- 6.
- Polynomet
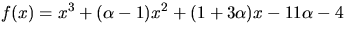 har
koefficienter i kroppen
har
koefficienter i kroppen 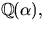 där
där
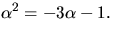 Man vet att
Man vet att 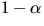 är ett nollställe till
f(x). Bestäm samtliga nollställen till f(x) i
är ett nollställe till
f(x). Bestäm samtliga nollställen till f(x) i 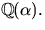
- 7.
- Beräkna summan
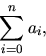
där de rationella talen an definieras rekursivt av
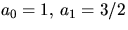 och an=3an-1/2-an-2/2, när
och an=3an-1/2-an-2/2, när 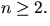
- 8.
- Bestäm en så liten kropp K som möjligt, som innehåller
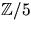 och är sådan att polynomet
och är sådan att polynomet ![$x^{4}+3x^{2}+4\in \mathbb Z/5[x]$](img15.gif) faktoriserar som en produkt av polynom av grad 1 i K[x].
faktoriserar som en produkt av polynom av grad 1 i K[x].
Förslag till svar:
4) 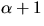 5)
5) 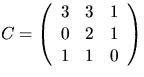 och
och
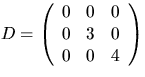 6)
6) 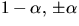 7) 2n+2-n 8)
7) 2n+2-n 8) 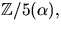 där
där
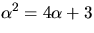 och
och 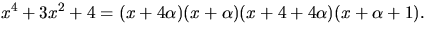
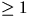 i K[x] kan
skrivas som en produkt av irreducibla polynom.
i K[x] kan
skrivas som en produkt av irreducibla polynom.
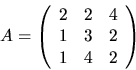
![]()
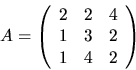
![]()
![]() 5)
5) 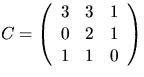 och
och
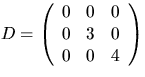 6)
6) ![]() 7) 2n+2-n 8)
7) 2n+2-n 8) ![]() där
där
![]() och
och ![]()