Tentamen i Aritmetik och algebra, del 2, 98 xx 02.
- 1.
- Visa att om en formell potensserie
![$f(x)\in K[[x]],$](img1.gif) där K är en
kropp, är inverterbar om och endast om
där K är en
kropp, är inverterbar om och endast om 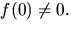
- 2.
- Formulera och bevisa Eisensteins kriterium.
- 3.
- (a)
- Vad menas med en största gemensam delare till två polynom i
K[x], där K är en kropp?
- (b)
- Formulera och bevisa Bezouts identitet för en största gemensam
delare till två polynom f och g.
- 4.
- Visa att
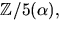 där
där 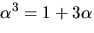 är en kropp
och invertera elementet
är en kropp
och invertera elementet 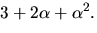
- 5.
- Bestäm en bas för lösningsrummet till ekvationssystemet
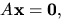 där
där
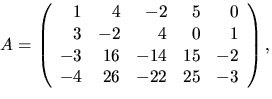
har element i 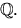
- 6.
- En talföljd i
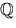 definieras rekursivt av
definieras rekursivt av
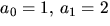 och
och
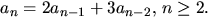 Beräkna
an.
Beräkna
an.
- 7.
- Bestäm en så liten kropp K som möjligt, som innehåller
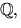 så att polynomet
så att polynomet
![$(x^2-3)(x^2+3x-1)\in \mathbb Q[x]$](img13.gif) faktoriserar som en produkt av
polynom av grad 1 i K[x]. Ange faktoriseringen i K[x].
faktoriserar som en produkt av
polynom av grad 1 i K[x]. Ange faktoriseringen i K[x].
- 8.
- Beräkna summan
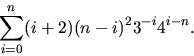
Förslag till svar
4) 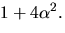 5) T.ex.
5) T.ex. 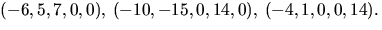
6) an=(3n+1+(-1)n)/4
7) T.ex. 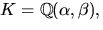 där
där 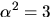 och
och
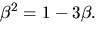
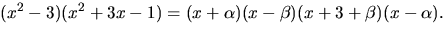
8) (84n-708)3-n+(6n2+120n+708)4-n.
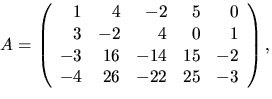
![]()
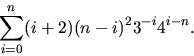
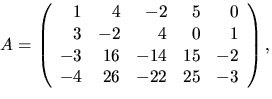
![]()
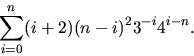
![]() 5) T.ex.
5) T.ex. ![]()
![]() där
där ![]() och
och
![]()
![]()