Tentamen i Aritmetik och algebra, del 2, 98 xx 05.
- 1.
- Visa att ett primitivt polynom i
![$\mathbb Z[x]$](img1.gif) är irreducibelt i
är irreducibelt i
![$\mathbb Z[x]$](img1.gif) om och endast om det är irreducibelt i
om och endast om det är irreducibelt i ![$\mathbb Q[x].$](img2.gif)
- 2.
- Visa att om K är en kropp och p(x) är ett irreducibelt polynom i
K[x], så är K[x]/p(x) en kropp.
- 3.
- Låt A vara en
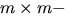 matris med koefficienter i kroppen K
och
matris med koefficienter i kroppen K
och 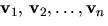 egenvektoer
till A som hör till olika egenvärden. Visa att egenvektorerna är
linjärt oberoende.
egenvektoer
till A som hör till olika egenvärden. Visa att egenvektorerna är
linjärt oberoende.
- 4.
- Visa att
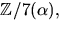 där
där 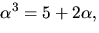 är en
kropp och invertera elementet
är en
kropp och invertera elementet 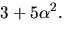
- 5.
- Visa att
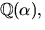 där
där 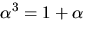 är en
kropp. Polynomet
är en
kropp. Polynomet
![$x^3+(3-3\alpha)x^2+(3-6\alpha-\alpha^2)x+4-\alpha^2\in \mathbb
Q(\alpha)[x]$](img10.gif) har nollställena
har nollställena 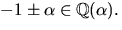 Bestäm polynomets samtliga nollställen i
Bestäm polynomets samtliga nollställen i 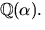
- 6.
- Beräkna An, där n är ett heltal
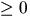 och
och
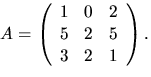
har element i 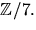
- 7.
- En talföljd i
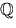 definieras rekursivt av
definieras rekursivt av
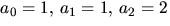 och
och
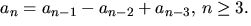 Beräkna an.
Beräkna an.
- 8.
- Bestäm produkten av
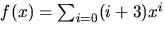 och
och
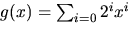 i
i ![$\mathbb Z/5[[x]].$](img21.gif)
Förslag till svar:
4) 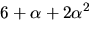 5)
5) 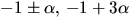 6)
6)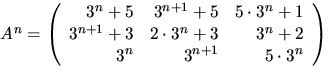 7) an=in(i-1+(-1)n+1(1+i))/4+3/2.
8)
7) an=in(i-1+(-1)n+1(1+i))/4+3/2.
8) 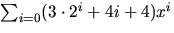
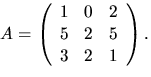
![]()
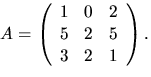
![]()
![]() 5)
5) ![]() 6)
6)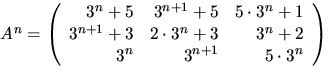 7) an=in(i-1+(-1)n+1(1+i))/4+3/2.
8)
7) an=in(i-1+(-1)n+1(1+i))/4+3/2.
8) ![]()