Datorlaboration 1 (D1) i Linjär Algebra

Om du har gått igenom MATLAB-handledningen vid något tidigare tillfälle, räcker det troligen med att du fräschar upp minnet.

1.
Gå igenom handledningens avsnitt 1,2 och 3 samt gör övningarna till dessa avsnitt.
2.
Gå igenom handledningens avsnitt 4 och 5 samt gör övningarna till dessa avsnitt.
Gör också minst en av de blandade uppgifterna till avsnitt 1-5.
3.
Gå igenom MATLAB-handledningens avsnitt 6.1 - 6.4. Vi rekommenderar att du skriver in olika matriser i en särskild textfil, typ ``matrisen.m'' i avsnitt 6.4.
4.
Skriv in följande matris i din fil:

\begin{displaymath} A=\left[ \begin{array} {rrrrrr} 6 & 5 & 4 & 3 & 2 & 1 \\ ... ...& 2 & 1 & 1 & 1 \\ 3 & 2 & 1 & 1 & 1 & 1 \end{array} \right]\end{displaymath}

 Använd nu kommandot $\gt\gt {\tt rref(A)}$ för att avgöra om kolonnerna i A spänner upp ${\Bbb R}^4$.
Skriv sedan in matrisen

\begin{displaymath} b=\left[ \begin{array} {r} 1\\ 2\\ 3\\ 4 \end{array} \right]\end{displaymath}

 och använd kommandot $\gt\gt {\tt rref(A)}$ för att finna alla lösningar till ekvationssytemet $A{\mathbf x}=b$.
5.
(a)
Kursbokens övning 1.1: 35 och 36 handlar om den stationära värmefördelningen i en platta. Gå igenom texten till dessa uppgifter, skriv upp det ekvationssystem som karakteriserar den stabila värmefördelningen och lös detta system. Skriv in ekvationssystemet i en särskild fil, så som du gjorde i föregående uppgift.
(b)
Välj fyra olika heltal T1,T2,T3,T4 bland talen 1,2,...,9.
Betrakta följande figur där T1,...,T4 vid randpunkterna anger randtemperatur. Finn den stationära värmefördelningen i den inringade punkten.
\includegraphics []{../../Figurer/varme.eps}

Redovisning
Kurssidan ger besked om senaste tidpunkt för redovisningen.
Redovisningen sker genom att ni på en A4-sida skriver
era namn (texta)
nummer på den grupparbetsgrupp som du tillhör
antalet fria variabler i systemet Ax=b i uppgift 2
de fyra valda talen T1,T2,T3,T4 (i denna ordning)
den stationära värmefördelningen i den inringade punkten.


Extra uppgifter för den intresserade

Sifferchiffer
Låt alfabetets stora bokstäver representera obekanta hela tal. Man kan då bilda ekvationer i stil med

N+O+L+L = 0,
E+T+T = 1,
T+V+Å = 2,
osv.

Höger led är alltså talen 0,1,2,3,.... Hur långt kan man gå utan att systemet blir olösbart? Kan man finna en lösning till det sista lösbara systemet där varje förekommande bokstav står för ett heltal? Kan man välja en lösning så att varje förekommande bokstav står för ett unikt heltal?

Vidareutveckla uppgift 2
Bilda den $m \times n-$ matris A vars rad nummer r, ($r=1,\ldots,m$) är

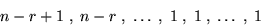
\begin{displaymath} n-r+1 \; , \; n-r \; , \; \ldots \;, \; 1 \;, \; 1 \;, \; \ldots \;, \; 1 \end{displaymath}

Vi antar att m<n. Finn alla lösningar till systemet $A{\mathbf x}=b$ där $b=(1,2,\ldots,m)$ för olika m och n.