|
Nyckelord |
Satser. |
Nyckelproblem |
|
Analytisk geometri. Punktmängderna |
Beräkna vektor som går från en punkt till annan punkt. Beräckna medelpunkt på en sträcka . Beräckna skärningspunkt av ett plan och en rätlinje. Skriv ekvationen för den linje som går genom två givna punkter. |
|
|
Skalärprodukt i plan i rummet ,linje i rummet och i plan.
|
Chauchys olikhet, Triangelolikhet. ( AG 1.3 ) |
Skriv ekvationen för det plan som går genom tre givna punkter. Beräkna proektion av en punkt på en linje, på ett plan. Beräkna avståndet från en punkt till en linje, till ett plan. |
|
Beräkna avståndet mellan två parallella plan, mellan två linjer. |
||
|
2x2 och 3x3 determinanter Vektorprodukt, trippelprodukt. |
Geometrisk betydelse av Trippelprodukt och krussprodukt. |
Bestämm om tre vektorer ligger i samma plan. Bestämm normalen till två givna vektorer. |
|
Linjära ekvationsystem. Lösningar. Existens. Entydighet. |
||
|
Matris. Rad operationer. Ekvivalenta system. Radekvivalenta matriser. |
||
|
Trappstegsform på matris. Pivot element. Pivot position. |
Sats om existens och entydighet. |
Omforma en matris till trappstegsform med radoperationer . Ange pivot element, pivot positioner. |
|
Gauss' elimination, direkt fas, bakåt fas. |
|
Lös ett linjärt ekvationsystem med Gauss' elimination. |
|
Allmänn lösning. S. 25 |
Satsen om allmänn lösning till ett linjärt system |
Ange fria variabler till ett linjärt system |
|
|
Hitta den almänna lösningen till ett system |
|
|
Linjär transformation. Standart matris |
Satsen om standart matris till en linjär transformation. |
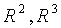 , Vektorer som parallellförfluttning i planet och rummet. Standartbaser i
, Vektorer som parallellförfluttning i planet och rummet. Standartbaser i 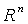 .
.