$\parbox{5cm}{Differentialgeometri\\ V 00 \\ ~~~~\\ ~~~~}$

Inlämningsuppgift 2

När A=A(s) är en kvadratisk matris vars element beror på variabeln s definieras

$$\mbox{e}^{A}=I+A/1!+A^{2}/2!+A^{3}/3!+\cdots$$

Låt B_i,j beteckna elementet i matrisen B på rad i och kolonn j.

Man kan se att funktionsserien $\sum_{k=0}^{\infty}(A^{k})_{i,j}/k!,$begränsad till ett slutet begränsat intervall, satisfierar Weierstrass majorantsats och alltså är likformigt konvergent. Seriens derivata är därför $\sum_{k=0}^{\infty} (A^{k})'_{i,j}/k!$.

I allmänhet finns det inget enkelt uttryck för denna derivata, av den anledning att $AA'\not=A'A,$ i allmänhet.

När A är av formen f(s)B där f är en reellvärd funktion och B är en konstant matris har vi emellertid A'A=f'(s)Bf(s)B=f(s)Bf'(s)B=AA' och (A^k)'=kA'A^k-1=kf'f^k-1B^k. Detta ger alltså

$$(\mbox{e}^{f(s)B})'=f'(s)B\mbox{e}^{f(s)B}$$

För att försöka beräkna $\mbox{e}^{f(s)B}$ kan man dra nytta av Cayley-Hamiltons sats: En matris satisfierar sin karaktäristiska ekvation.

1.

Antag att

$$B=\left(\begin{array} {rrr} 0 & -1 & 0\\ 1 & 0 & c\\ 0 & -c & 0\\ \end{array}\right),$$

där c är en konstant. Visa att B³=-a²B, där $a=\sqrt{1+c^{2}}$.

2.

Visa att

$$\mbox{e}^{f(s)B}=I+(\sin(af(s))/a)B-((\cos(af(s))-1)/a^{2})B^{2}.$$

3.

Antag att $\alpha(s)$ är en reguljär kurva parametriserad med båglängd sådan att k(s)>0 och $\tau(s)/k(s)$ är konstant c. Visa att om Frenets treben till kurvan i s=0 är standardbasen för $\mathbb R^{3},$ så är

$$t(s)=(c^{2}/a^{2}+\cos(aK(s))/a^{2},-\sin(aK(s))/a,c(\cos(aK(s))-1)/a^{2})$$

där K(s) är en primitiv funktion till k(s) med K(s)=0. (Lös Frenets ekvationer.)

4.

Visa att för en lämplig rotation R är $Rt(s)=(-\sin(aK(s))/a,\cos(aK(s))/a,c/a)$.

5.

Antag nu att $k(s)=1/\sqrt{2-2s^{2}}$ och att $c=\tau/k=1$. Bestäm $\alpha$ om att om $\alpha(0)=0$ och $t(s)=(-\sin(aK(s))/a,\cos(aK(s))/a,c/a)$.

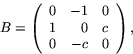
[10cm,2cm]kamel.ps [7cm,2cm]kamel1.ps

Figur 1 illustrerar kurvan $\alpha$ medan figur 2 visar .