- (a)
- Om
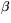 är en reguljär kurva ges krökning och torsion av
är en reguljär kurva ges krökning och torsion av
Vi har enligt Frenets ekvationer (med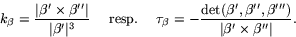
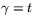 )
)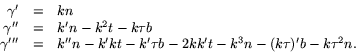
Detta ger
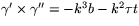 och sen
och sen
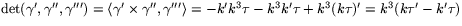 och
och 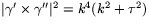 .
.Vi får alltså att
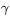 har krökning och torsion
har krökning och torsion
Vilket visar påståendet i uppgiften.H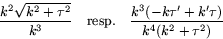
- (b)
- Eftersom
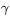 är en kurva på
S2 räcker det att visa att
är en kurva på
S2 räcker det att visa att 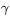 är plan precis när
är plan precis när 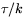 är konstant. Vi har enligt ovan att
är konstant. Vi har enligt ovan att 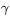 är reguljär (krökningen
positiv), så det räcker att visa att kurvans torsion är precis när
är reguljär (krökningen
positiv), så det räcker att visa att kurvans torsion är precis när
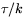 är konstant. Men båda inträffar precis när
är konstant. Men båda inträffar precis när
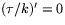 . Vilket visar påståendet.
. Vilket visar påståendet.
- (a)
- Eftersom f i själva verket är defnerad som en funktion
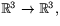 med uppenbart glatta
koordinatfunktioner, räcker det för att visa att
med uppenbart glatta
koordinatfunktioner, räcker det för att visa att
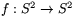 är glatt att |f(p)|2=1 när
|p|2=1.
är glatt att |f(p)|2=1 när
|p|2=1.
Antag alltså att p=(x,y,z) och att |p|2=1. Vi har då |f(p)|2=((x2-y2)2+4x2y2+z2)/(z4-z2+1)= ((x2+y2)2+z2)/(z4-z2+1)=((1-z2)2+z2)/(z4-z2+1)=1.
Jacobianen dfp av funktionen
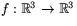 ges av matrsen
ges av matrsen
där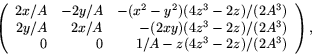
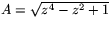 .
.Vi väljer nu basen e1(p)=(y,-x,0) och
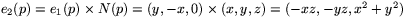 för tangentrummet
Tp(S2). Avbildningen dfp (p=(x,y,z)) ger oss följande vektorer i
Tf(p)(S2):
för tangentrummet
Tp(S2). Avbildningen dfp (p=(x,y,z)) ger oss följande vektorer i
Tf(p)(S2):
Vi ser att dfp(e1(p))=2e1(f(p)). Eftersom e1 har längd 1, medan df(e1) har längd 2 kan dfp inte vara en isometri.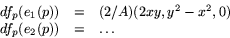
Räkningarna ovan förutsätter att
 I dessa båda
fall kan vi välja e1=(1,0,0) och e2(0,1,0). Vi har då
df(e1)=(0,0,0), så dfp kan inte ens vara en isomorfi i
dessa fall.
I dessa båda
fall kan vi välja e1=(1,0,0) och e2(0,1,0). Vi har då
df(e1)=(0,0,0), så dfp kan inte ens vara en isomorfi i
dessa fall.
- (a)
- Vi har uq(v)+(1-u)p(v)=(u,v,(1-u)v3/3)
En grafparametrisering av S ges av
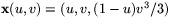 . Därmed är S en reguljär orienterbar
yta.
. Därmed är S en reguljär orienterbar
yta.
- (b)
- Vi har
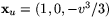 och
och 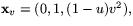 så
så 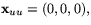
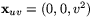 och
och 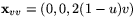 .
.Detta ger E=1+v6/9, F=-(1-u)v5/3 och G=1+(1-u)2v4 samt e=0,
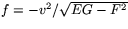 och
och
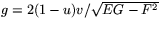 . Vi får därför
. Vi får därför
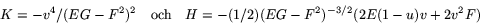
Av detta följer att pukter där
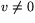 är hyperboliska. I punkter där
v=0 är K=H=0, så dessa punkter är plana (och navelpunkter).
är hyperboliska. I punkter där
v=0 är K=H=0, så dessa punkter är plana (och navelpunkter).
- (c)
- Differentialekvationen för asymptotiska kurvor blir
0=2v2u'v'+2(1-u)v(v')2=vv'(2vu'+2(1-u)v')
Alternativet v'=0, ger v=k, där k är en konstant, medan 0=2v2u'+2(1-u)vv' efter separering och integrering ger
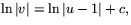 (c en konstant) så v=C(u-1), där C är en
godtycklig konstant. De asymptotiska kurvorna är alltså dels
(c en konstant) så v=C(u-1), där C är en
godtycklig konstant. De asymptotiska kurvorna är alltså dels
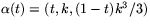 och dels
och dels
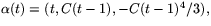 där k och C är godtyckliga konstanter.
där k och C är godtyckliga konstanter.
- (a)
- Villkoret att linjen genom
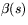 och
och 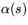 är vinkelrät
mot kurvan
är vinkelrät
mot kurvan 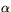 ger att vi måste ha
ger att vi måste ha
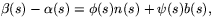 för några funktioner
för några funktioner
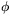 och
och 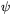 .
.Villkoret att linjen genom
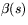 och
och 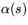 är tangentlinje
till
är tangentlinje
till 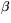 ger att
ger att 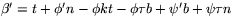 är parallell med
är parallell med 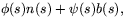 så vi får speciellt
så vi får speciellt
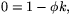 eller
eller 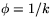 . Villkoret blir sedan att
. Villkoret blir sedan att
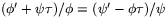 . Men
. Men 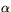 är
reguljär och plan, så
är
reguljär och plan, så 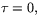 så vi får istället
så vi får istället
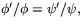 eller
eller 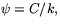 där C är en godtycklig
konstant.
där C är en godtycklig
konstant.
Svar:
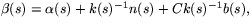 där C är en godtycklig konstant.
där C är en godtycklig konstant.
- (b)
- Vi har
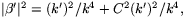 så alla evolutor är
reguljära när
så alla evolutor är
reguljära när 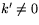 .
. - (c)
- En reguljär kurva
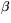 är plan när
är plan när
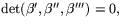 för då är dess torsion =0.
för då är dess torsion =0.
Vi har
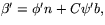
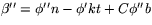 och
och 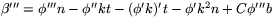 .
.Detta ger
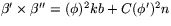 och därmed
är
och därmed
är 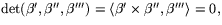 precis när C=0.
precis när C=0.