
Förslag till lösning av inlämningsuppgift 2
- 1.
- Matrismultiplikation ger
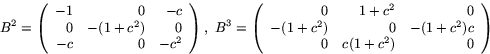
så om 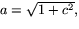 så är B3=-a2B.
så är B3=-a2B.
- 2.
- Av B3=-aB får vi B2k=-(-1)ka2k-2B2 och
B2k+1=(-1)ka2kB, så
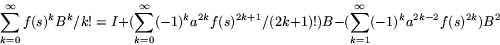
Men Taylor utvecklingarna för 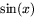 och
och  är
är
så vi får
- 3.
- Frenets ekvationer är i matrisformulering
Vi vet att 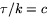 är konstant, så om vi sätter
är konstant, så om vi sätter
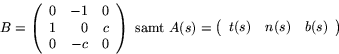
kan ekvationerna skrivas A'(s)=A(s)k(s)B. Enligt fundamentalsaten
för kurvor har detta ekvationssystem precis en lösning A(s) om vi
kräver A(0)=I (Frenets treben standardbasen för  när
s=0). Låt nu K(s) vara en primitiv funktion till k(s) med s=0.
Vi har då
när
s=0). Låt nu K(s) vara en primitiv funktion till k(s) med s=0.
Vi har då
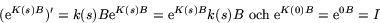
Vi ser att 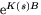 är en (den enda) lösningen till
problemet. Den fösta kolonnen i
är en (den enda) lösningen till
problemet. Den fösta kolonnen i 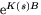 är
är
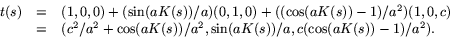
- 4.
- Villkoret för att R ska vara en rotation är att kolonnerna är
av längd 1 och ömsesidigt ortogonala och att matrisen har
determinant 1.
Vi prövar oss fram till den sökta rotationen genom
att konstatera att om första raden är 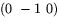 får vi rätt
x-koordinat i Rt(s). Om andra raden är
får vi rätt
x-koordinat i Rt(s). Om andra raden är 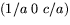 stämmer även
y-koordinaten. Väljer vi
stämmer även
y-koordinaten. Väljer vi 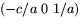 som tredje rad i R
får vi rätt z-koordinat. Kontroll visar att R är ortogonal.
som tredje rad i R
får vi rätt z-koordinat. Kontroll visar att R är ortogonal.
- 5.
- En primitiv funktion till k(s) är
 . Vi har också
. Vi har också 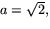 så formeln för
tangentvektorn är (
så formeln för
tangentvektorn är (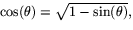 när
när
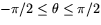 )
)
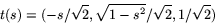
Vi bestämmer en primitiv funktion till 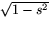 (kan göras på
flera olika sätt) genom variabelsubstitution:
(kan göras på
flera olika sätt) genom variabelsubstitution:
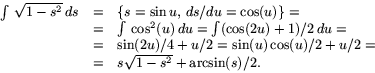
Detta tillsammans med villkoret 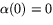 ger nu
ger nu
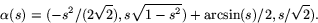
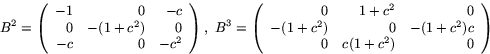
![]()
![]()
![]()
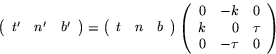
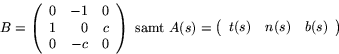
![]()
![]()
![]() får vi rätt
x-koordinat i Rt(s). Om andra raden är
får vi rätt
x-koordinat i Rt(s). Om andra raden är ![]() stämmer även
y-koordinaten. Väljer vi
stämmer även
y-koordinaten. Väljer vi ![]() som tredje rad i R
får vi rätt z-koordinat. Kontroll visar att R är ortogonal.
som tredje rad i R
får vi rätt z-koordinat. Kontroll visar att R är ortogonal.
![]()
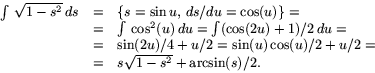
![]()
