- 1.
- Om vi sätter
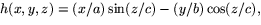 så är h(p)=0,
när p ligger på helikoiden.
Om å andra sidan h(x,y,z)=0, så är (x/a,y/b) vinlekrät mot
så är h(p)=0,
när p ligger på helikoiden.
Om å andra sidan h(x,y,z)=0, så är (x/a,y/b) vinlekrät mot
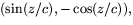 dvs parallell med
dvs parallell med 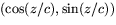 .Sätter vi u=z/c betyder detta att
.Sätter vi u=z/c betyder detta att 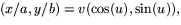 för något
för något 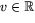 . Detta ger nu att
. Detta ger nu att
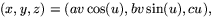 så att punkten ligger på
helikoiden. Därmed är helikoiden precis h-1(0).
så att punkten ligger på
helikoiden. Därmed är helikoiden precis h-1(0).
De kritiska punkterna till h är de där 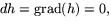 vilket ger
ekvationssystemet 0=h'x=h'y=h'z eller
vilket ger
ekvationssystemet 0=h'x=h'y=h'z eller
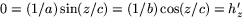 . De två första ekvationerna
saknar samtidig lösning z, så h saknar kritiska punkter.
. De två första ekvationerna
saknar samtidig lösning z, så h saknar kritiska punkter.
Alltså är ett reguljärt värde till h och helikoiden h-1(0)
en reguljär yta.
- 2.
- Funktionen f definierar en glatt avbildning
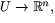 där U är den öppna delmängd till
där U är den öppna delmängd till 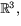 där
där 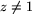 , eftersom koordinatfunktionerna har kontinuerliga
partialderivator av godtycklig ordning i varje punkt i U.
, eftersom koordinatfunktionerna har kontinuerliga
partialderivator av godtycklig ordning i varje punkt i U.
Det räcker därför att visa att 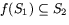 . Men om vi
i definitionen av helikoiden sätter v=y/(1-z) och u=x/(1-z) ser
vi att
. Men om vi
i definitionen av helikoiden sätter v=y/(1-z) och u=x/(1-z) ser
vi att 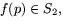 för varje
för varje 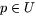 . Speciellt är
. Speciellt är
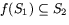 .
.
- 3.
- Eftersom S2 är g-1(0), där
g(x,y,z)=x2+y2+z1-1 har som reguljärt värde, är en
normal till tangentrummet i p=(x,y,z) parallell med gradienten
till g som är (2x,2y,2z). Vi ser att p är en normal till
tangentrummet Tp(S1)=Tp(S2).
För att visa att v1(p) och v2(p) ligger i tangentrummet
räcker det att visa att de är vinkelräta mot p=(x,y,z). Vi får
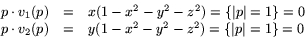
För att visa att de är linjärt oberoende kan vi konstatera att
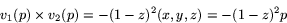
inte är 0, när 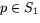 . Därmed bildar de en bas för det
tvådimensionella tangentrummet Tp(S1).
. Därmed bildar de en bas för det
tvådimensionella tangentrummet Tp(S1).
För att visa att w1(p) och w2(p) kan man göra på samma sätt
genom att använda att 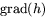 (från 1)) är en normal till
tangentrummet. Vi väljer i stället, för variationens skull, att
konstatera att
(från 1)) är en normal till
tangentrummet. Vi väljer i stället, för variationens skull, att
konstatera att 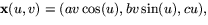
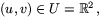 är en
parametrisering av helikoiden. Vi ser att
är en
parametrisering av helikoiden. Vi ser att 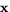 är glatt med
är glatt med
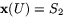 öppen i S2. Vidare är den injektiv, för
öppen i S2. Vidare är den injektiv, för
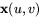 bestämmer u entydigt i tredje koordinaten och sedan
är
bestämmer u entydigt i tredje koordinaten och sedan
är 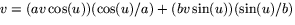 .
.
Eftersom vi redan vet att S2 är en reguljär yta räcker det att
visa att 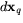 är injektiv, eller ekvivalent
är injektiv, eller ekvivalent 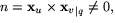 för varje
för varje 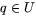 . Vi får
. Vi får
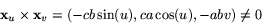
Alltså är 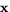 en lokal parametrisering av S2 och n är
en normal till tangentrummet (som spänns av
en lokal parametrisering av S2 och n är
en normal till tangentrummet (som spänns av 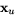 och
och
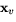 ).
).
Om 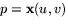 har vi
har vi
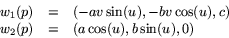
som båda är vinkelräta mot n. För att visa att de utgör en bas
räcker det nu att konstatera att
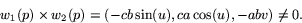
- 4.
- Eftersom
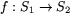 är restriktion av en glatt
avbildning
är restriktion av en glatt
avbildning 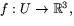 där
där 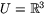 är den öppna
mängden där
är den öppna
mängden där 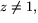 kan vi beräkna dfp(w), genom att
använda Jakobis matris (i standardbasen) för df, där
kan vi beräkna dfp(w), genom att
använda Jakobis matris (i standardbasen) för df, där 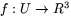 . Den är
. Den är 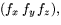 som om vi
sätter
som om vi
sätter 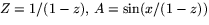 och
och 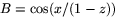 blir
blir
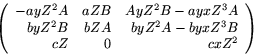
När p=(0,1,0) är 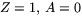 och B=0, så
och B=0, så
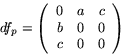
Vidare har vi v1(p)=(1,0,0), v2(p)=(0,0,1), f(p)=(a,b,0),
w1(f(p))=(-a,b,c) samt w2(f(p))=(a,0,0).
Vi får dfp(v1)=(0,b,c)=w1+w2 och
dfp(v2)=(a,0,0)=w2.
Matrisen för dfp relativt de angiva baserna blir därför
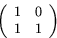
- 5.
- För att visa att f är en bijektion ska vi, för varje punkt
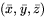 på helikoiden, visa att det finns en
entydig punkt (x,y,z) på S1, sådan att
på helikoiden, visa att det finns en
entydig punkt (x,y,z) på S1, sådan att 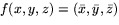 .
.
Av denna ekvation får vi
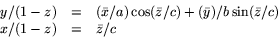
Eftersom vi söker lösa problemet så att x2+y2+z2=1 har vi
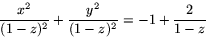
Använder vi detta och utnyttjar att 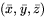 ligger på
helikoiden
ligger på
helikoiden 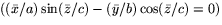 får
vi
får
vi
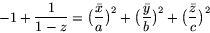
Om vi sätter 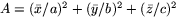 , får vi 1-z
=2/(A+1). Inversen till f ges alltså av
, får vi 1-z
=2/(A+1). Inversen till f ges alltså av
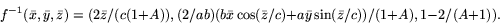
Vi ser att detta uttryck definierar en glatt funktion från
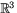 till
till 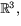 eftersom koordinatfunktionerna
har kontinuerliga partialderivator av godtycklig ordning. Där med är
restriktionen av denna,
eftersom koordinatfunktionerna
har kontinuerliga partialderivator av godtycklig ordning. Där med är
restriktionen av denna, 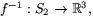 glatt. Eftersom
glatt. Eftersom 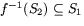 har vi att f-1 är
glatt, och därmed är f en diffeomorfi.
har vi att f-1 är
glatt, och därmed är f en diffeomorfi.
![]() vilket ger
ekvationssystemet 0=h'x=h'y=h'z eller
vilket ger
ekvationssystemet 0=h'x=h'y=h'z eller
![]() . De två första ekvationerna
saknar samtidig lösning z, så h saknar kritiska punkter.
. De två första ekvationerna
saknar samtidig lösning z, så h saknar kritiska punkter.
![]() . Men om vi
i definitionen av helikoiden sätter v=y/(1-z) och u=x/(1-z) ser
vi att
. Men om vi
i definitionen av helikoiden sätter v=y/(1-z) och u=x/(1-z) ser
vi att ![]() för varje
för varje ![]() . Speciellt är
. Speciellt är
![]() .
.![]()
![]()
![]() (från 1)) är en normal till
tangentrummet. Vi väljer i stället, för variationens skull, att
konstatera att
(från 1)) är en normal till
tangentrummet. Vi väljer i stället, för variationens skull, att
konstatera att ![]()
![]() är en
parametrisering av helikoiden. Vi ser att
är en
parametrisering av helikoiden. Vi ser att ![]() är glatt med
är glatt med
![]() öppen i S2. Vidare är den injektiv, för
öppen i S2. Vidare är den injektiv, för
![]() bestämmer u entydigt i tredje koordinaten och sedan
är
bestämmer u entydigt i tredje koordinaten och sedan
är ![]() .
.![]() är injektiv, eller ekvivalent
är injektiv, eller ekvivalent ![]() för varje
för varje ![]() . Vi får
. Vi får
![]()
![]() har vi
har vi
![]()
![]()
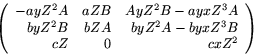
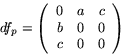
![]()
![]()
![]()
![]()
![]()
![]() till
till ![]() eftersom koordinatfunktionerna
har kontinuerliga partialderivator av godtycklig ordning. Där med är
restriktionen av denna,
eftersom koordinatfunktionerna
har kontinuerliga partialderivator av godtycklig ordning. Där med är
restriktionen av denna, ![]() glatt. Eftersom
glatt. Eftersom ![]() har vi att f-1 är
glatt, och därmed är f en diffeomorfi.
har vi att f-1 är
glatt, och därmed är f en diffeomorfi.
