
Förslag till lösning av inlämningsuppgift 5
- 1.
- funktionen f(x,y,z)=x2+y2-1 är en glatt funktion från
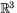 till
till 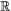 med gradient (2x,2y,0). De
kritiska punkterna till f är (0,0,z) och f antar inte värdet
i någon av dessa. Alltså är cylindern f-1(0) en reguljär
orienterbar yta. En Gaussavbildning ges av
med gradient (2x,2y,0). De
kritiska punkterna till f är (0,0,z) och f antar inte värdet
i någon av dessa. Alltså är cylindern f-1(0) en reguljär
orienterbar yta. En Gaussavbildning ges av
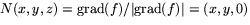 som pekar ``ut''
från ytan.
som pekar ``ut''
från ytan.
- 2.
- För parametriseringen
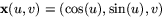 har vi
har vi
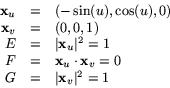
- 3.
- Vi kan anta att
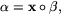 där
där
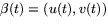 är en kurva i u,v-planet. Villkoret i
uppgiften är att
är en kurva i u,v-planet. Villkoret i
uppgiften är att 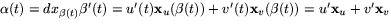 ska ha vinkeln t med vektorn
e3=(0,0,1). Vi ska alltså ha
ska ha vinkeln t med vektorn
e3=(0,0,1). Vi ska alltså ha
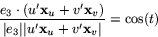
Eftersom 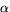 ska vara båglängdsparametriserad ska vi ha
ska vara båglängdsparametriserad ska vi ha 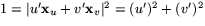 .
Insättning av detta och uttrycken för
.
Insättning av detta och uttrycken för 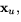 samt
samt 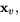 ger oss därför
ger oss därför 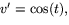 eller
eller
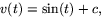 där c är en konstant.
där c är en konstant.
Från (u')2+(v')2=1, får vi sedan att 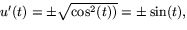 eller
eller 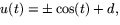 där d är
en konstant. Lösningarna till problemet är alltså
där d är
en konstant. Lösningarna till problemet är alltså
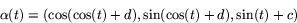
där c,d är godtyckliga reella tal. (Muinustecknet spelar ingen roll
i 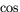 .)
.)
- 4.
- Vi väljer
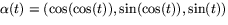 . Eftersom
. Eftersom
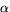 är parametriserad med båglängd ges krökningen av
är parametriserad med båglängd ges krökningen av 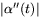 och normalkrökningen av
och normalkrökningen av 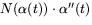 .
Vi får
.
Vi får
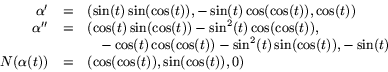
Detta ger oss
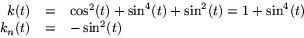
Jan-Alve Svensson
2/25/2000
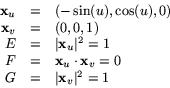
![]()
![]() eller
eller ![]() där d är
en konstant. Lösningarna till problemet är alltså
där d är
en konstant. Lösningarna till problemet är alltså
![]()
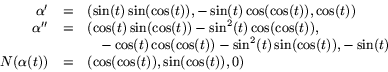
![]()

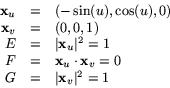
![]()
![]() eller
eller ![]() där d är
en konstant. Lösningarna till problemet är alltså
där d är
en konstant. Lösningarna till problemet är alltså
![]()
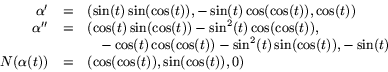
![]()