En (graf)parametrisering av ytan ges av ![]() . Vi beräknar krökningarna med hjälp av denna:
. Vi beräknar krökningarna med hjälp av denna:
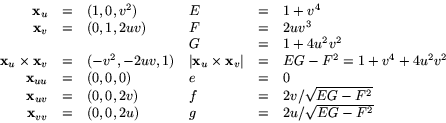
Vi får
![]()
Vi ser att ![]() så elliptiska punkter saknas. Vi har K=0, bara
när v=0, som ger H=u, så
så elliptiska punkter saknas. Vi har K=0, bara
när v=0, som ger H=u, så ![]() är parabolisk när
är parabolisk när
![]() och plan när u=0.
och plan när u=0.
I en navelpunkt ska vi ha K=H2, så vi ska ha K=0 (eftersom
![]() ), samt H=0. Ytan har alltså precis en
navelpunkt:(0,0,0).
), samt H=0. Ytan har alltså precis en
navelpunkt:(0,0,0).
De asymptotiska linjerna är därför de reguljära kurvorna
![]()
Det sista är uppenbart. Att ![]() är injektiv följer av att
den andra koordinaten bestämmer u entydigt och att den första då
bestämmer v entydigt. Att
är injektiv följer av att
den andra koordinaten bestämmer u entydigt och att den första då
bestämmer v entydigt. Att ![]() är glatt följer av
inspektion av koordinatfunktionerna.
är glatt följer av
inspektion av koordinatfunktionerna.
Vi har
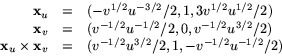
Differentialekvationen för asymptotiska linjer (i lokala koordinater) är e(u')2+2fu'v'+g(v')2, så vi beräknar e, f och g:
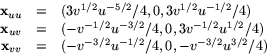
0=u'v'
Vi ser att detta löses av u=c och v=c, där c är en konstant. Koordinatkurvorna är alltså asymptotiska linjer.