![]()
Vi söker trajektorior till vektor fältet genom att ansätta
![]() där
där ![]() och z är funktioner som beror på
t. Vi ska ha
och z är funktioner som beror på
t. Vi ska ha ![]() vilket ger x=A,
vilket ger x=A,
![]() och
och ![]() där A, B och C är
konstanter. Eftersom
där A, B och C är
konstanter. Eftersom ![]() ska ligga på S ska vi ha
ska ligga på S ska vi ha
![]()
![]()
Vi försöker välja de räta linjerna från förra deluppgiften som
generatriser för regelytan och ska alltså söka w(t), så att
![]() .
.
För att få ![]() ska vi välja v=0, A=1+t2 och
y=-t. Jämför vi nu de tredje koordinaterna ser vi att vi ska välja
ska vi välja v=0, A=1+t2 och
y=-t. Jämför vi nu de tredje koordinaterna ser vi att vi ska välja
![]() . Linjen
(1+t2,y, -y(1+t2)/t)=(1+t2,0,0)+y(0,1,-(1+t2)/t) har
riktningsvektorn w(t)=(t,-(1+t2)).
. Linjen
(1+t2,y, -y(1+t2)/t)=(1+t2,0,0)+y(0,1,-(1+t2)/t) har
riktningsvektorn w(t)=(t,-(1+t2)).
Regelytan ![]() har nu lösningarna till
x2y2-xz2+z2=0,
har nu lösningarna till
x2y2-xz2+z2=0, ![]() som spår.
som spår.
Vi beräknar de ingående storheterna och använder att
f=(t2+(1+t2)2)-1/2 ger oss f'=-f3(3t+2t3):
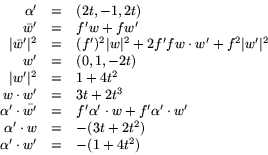
Tillsammans ger nu detta
![]()
Utnyttjar vi nu att (f'/f)2=f4(3t+2t3)2=-f'f(3t+2t3), ser vi att u=1/f.
Centrallinjen är alltså
![]()
Vi parametriserar om med
![]() . Distributionsparametern ges av
. Distributionsparametern ges av
![]()
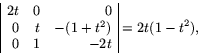
![]()
![]()
