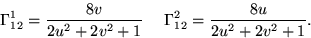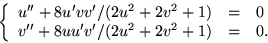![]()
![]()
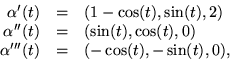
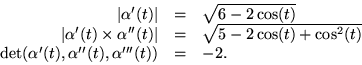
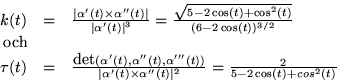
![]()
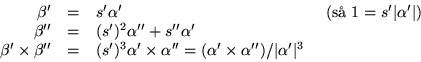
![]()
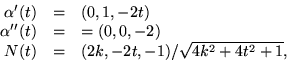
Den geodetiska krökningen blir alltså
![]()
- (a)
- Vi försöker visa att
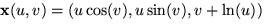 är en reguljär homeomorfi från
är en reguljär homeomorfi från
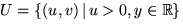 till
till 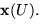
Vi har
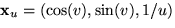 och
och 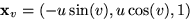 och
och 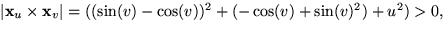 så
så 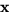 är reguljär.
är reguljär.
Om
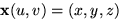 är
är 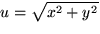 och
och
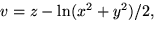 så
så 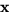 har en kontinuerlig
invers. Därmed är
har en kontinuerlig
invers. Därmed är 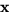 en (lokal) parametrisering av
en (lokal) parametrisering av
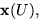 som alltså är en reguljär yta.
som alltså är en reguljär yta.
- (b)
- Vi bestämmer
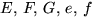 och g.
och g.
Detta ger nu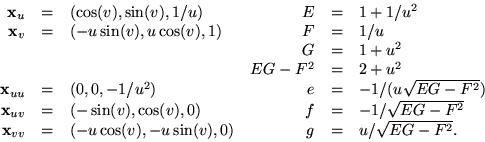
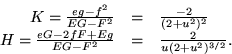
- (c)
- Av formeln för K ser vi att alla punkter är hyperboliska.
En bas för ![]() ges av
ges av ![]() och
och ![]() . Vi kan skriva
. Vi kan skriva ![]() för några reellvärda glatta
funktioner. Vi får
för några reellvärda glatta
funktioner. Vi får
![]()
Av detta följer att
![]()
- (a)
- (Se kurlitteraturen)
- (b)
- Vi har
Vi ser att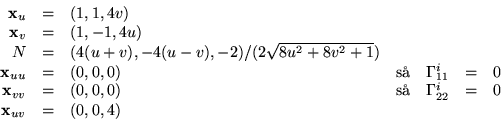
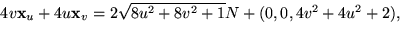 så
så
och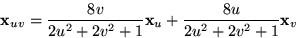
Differentialekvationen blir därför