- (a)
- Låt S vara en reguljär orienterbar yta med Gaussavbildning
N. Hur definieras normalkrökningen av en reguljär kurva C på
S i punkten p?
- (b)
- Visa att Weingartenavbildningen -dNp är självadjungerad.
- (c)
- Hur definieras Gausskrökningen och medelkrökningen av S i p?
- (d)
- Visa att summan av normalkrökningarna i två ortogonal
riktningar (tangentvektorer av längd 1) är 2H(p).
- (a)
- Hur definieras krökning och torsion av en reguljär båglängdsparametriserad kurva?
- (b)
- Härled Frenets ekvationer och visa att det finns, så när som på translation och rotation, precis en kurva med given krökning och torsion.
- (c)
- Uttryck krökningen och torsionen av en godtycklig reguljär
parametriserade kurva
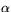 med hjälp av storheterna
med hjälp av storheterna 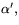
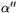 samt
samt 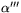 .
.
- (a)
- Visa att mängden av punkter av formen (u(v2+1),uv,(1-u)v),
där
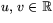 är en reguljär orienterbar yta S.
är en reguljär orienterbar yta S.
- (b)
- Bestäm de asymptotiska kurvorna på S.
- (c)
- Har S några navelpunkter, plana punkter eller paraboliska punkter?
- (a)
- Bestäm den geodetiska krökningen av kurvan
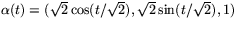 på ytan S av lösningar till x2+y2=z2+1. (Välj själv
normal till ytan.)
på ytan S av lösningar till x2+y2=z2+1. (Välj själv
normal till ytan.)
- (b)
- Låt P vara parallelltransport längs
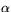 från
från
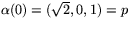 till
till
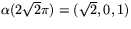 . Ange en bas för Tp(S) och bestäm P med hjälp av denna.
. Ange en bas för Tp(S) och bestäm P med hjälp av denna.
- (a)
- Låt S vara en reguljär yta och
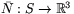 en glatt funktion, sådan att
en glatt funktion, sådan att 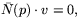 när
när
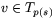 .
.Visa att om
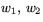 är en bas för Tp(S), så kan ytans
medelkrökning (relativt normeringen av
är en bas för Tp(S), så kan ytans
medelkrökning (relativt normeringen av 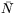 ) bestämmas som
) bestämmas som
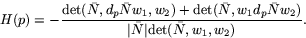
- (b)
- Bestäm medelkrökningen av den reguljära ytan som består av lösningarna till xyz=1. (Välj själv normal.)
- (a)
- Visa att det för varje funktion k(s)>0,
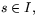 och
och 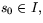 finns en
båglängdsparametriserad kurva
finns en
båglängdsparametriserad kurva 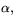 definierad i en omgivning av
s0, med egenskapen att
normalplanet i varje punkt
definierad i en omgivning av
s0, med egenskapen att
normalplanet i varje punkt 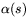 tangerar enhetssfären och att
är kurvans krökning är en restriktion av k. (Det
är alltså inte säkert att
tangerar enhetssfären och att
är kurvans krökning är en restriktion av k. (Det
är alltså inte säkert att 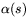 är definierat för på hela I.)
är definierat för på hela I.)
- (b)
- Vilka är de möjliga värdena på en sådan kurvas torsion?