- (a)
- Definiera begreppen tangent, normal och binormal, krökning och torsion till kurvan.
- (b)
- Härled, under lämplig förutsättning, Frenets ekvationer för
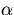 .
.
- (a)
- Visa att regelytan är reguljär om
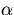 är en asymptotisk
kurva på S.
är en asymptotisk
kurva på S.
- (b)
- Visa att
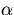 är en geodet på regelytan om och endast om den är
en asymptotisk kurva på S.
är en geodet på regelytan om och endast om den är
en asymptotisk kurva på S.
- (c)
- Uttryck Gausskrökningen för regelytan med
storheter som bara beror på
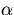 (och (t,v)) när
(och (t,v)) när 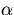 är
en asymptotisk kurva på S.
är
en asymptotisk kurva på S.
- (a)
- Visa att skruvytan är en reguljär orienterbar yta.
- (b)
- Låt
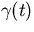 vara en geodet på S, och
vara en geodet på S, och 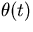 vinkeln
mellan
vinkeln
mellan 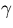 och koordinatkurvan v=konstant genom
och koordinatkurvan v=konstant genom
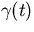 . Visa att
. Visa att
där v(t) är avståndet mellan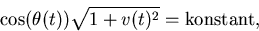
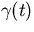 och z-axeln.
och z-axeln.
Bestäm alla isometrier ![]() .
.
- (a)
- Visa att parallelltransport av vektorer längs
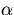 definierar en isometri
definierar en isometri
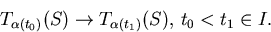
- (b)
- Välj basen
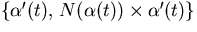 i
i
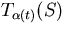 . Visa att parallelltransporten längs
. Visa att parallelltransporten längs 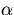 med detta basval har matrisen
med detta basval har matrisen
där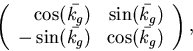
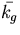 är en primitiv funktion till den geodetiska
krökningen av
är en primitiv funktion till den geodetiska
krökningen av 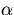 med
med 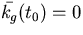 .
. - (c)
- Låt S vara ellipsoiden x2+y2+z2/4=1 och C
den slutna reguljära kurva som uppstår när S skärs med planet
z=1. Beräkna parallelltransporten ett varv längs kurvan. (Välj
en orientering.)