- (a)
- Beräkna kurvans krökning och torsion.
- (b)
- Visa att S är en reguljär yta som innehåller
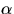 när
t>0 och
beräkna den geodetiska krökningen av
när
t>0 och
beräkna den geodetiska krökningen av 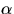 relativt S. (Välj
själv normal.)
relativt S. (Välj
själv normal.)
- (a)
- I vilka punkter är ytans Gausskrökning ?
- (b)
- Hur många plana punkter har ytan?
- (c)
- Avgör om
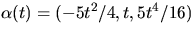 är en
asymptotisk kurva på S.
är en
asymptotisk kurva på S.
- (a)
- Visa att
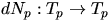 är självadjungerad.
är självadjungerad.
- (b)
- Visa att
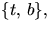 där t och b är
där t och b är 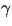 's tangent
respektive binormal, är en bas för tangentrummet.
's tangent
respektive binormal, är en bas för tangentrummet.
- (c)
- Antag att S har Gausskrökning K=0. Visa att
medelkrökningen H i
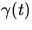 ges av
ges av
där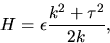
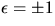 medan k och
medan k och 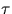 är krökningen
respektive torsionen av
är krökningen
respektive torsionen av 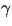 .
.
- (a)
- Visa att man kan välja en sådan parametrisering så att
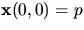 och
och 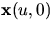 är parametriserad med båglängd.
är parametriserad med båglängd.
- (b)
- Visa att om S har konstant Gausskrökning K=0, så kan den lokala parametriseringen dessutom väljas så att koordinatkurvorna v= konstant är asymptotiska kurvor
- (c)
- Visa att dessa asymptotiska kurvor är räta linjer.
Efter skrivningstidens slut finns förslag till lösningar på kursens webb-sida. Skrivningen beräknas vara färdigrättad tisdagen den 13 april.