Tentamen i MAN500 Differentialgeometri,
99 08 18, kl 8.45-13.45.
- 1.
- Visa att alla normalplanen till kurvan
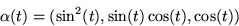
går genom origo.
- 2.
- Bestäm krökningen och torsionen av kurvan
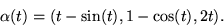
- 3.
- Låt S vara ytan x2-y2=z. Bestäm den geodetiska krökningen av
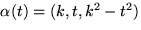 på S, där k är en konstant.
på S, där k är en konstant.
- 4.
- (a)
- Visa att
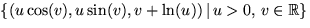 är en reguljär orienterbar yta.
är en reguljär orienterbar yta.
- (b)
- Bestäm ytans Gausskrökning och medelkrökning. (Välj själv
normal.)
- (c)
- Karaktärisera ytans punkter.
- 5.
- Antag att
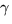 är en glatt kurva på den reguljära orienterbara
ytan S, med positiv krökning.
Visa att om
är en glatt kurva på den reguljära orienterbara
ytan S, med positiv krökning.
Visa att om 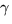 är en geodet och en krökningslinje, så
är
är en geodet och en krökningslinje, så
är 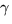 en plan kurva.
en plan kurva.
- 6.
- (a)
- Låt S vara en reguljär orienterbar yta med den lokala
parametriseringen
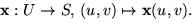 Härled en differentialekvation för u(t) och v(t), sådan
att
Härled en differentialekvation för u(t) och v(t), sådan
att 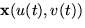 är en geodet på S om ekvationen satisfieras.
är en geodet på S om ekvationen satisfieras.
- (b)
- Bestäm differentialekvationen när S är ytan x2-y2=z
och

![]()
![]()
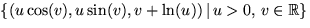 är en reguljär orienterbar yta.
är en reguljär orienterbar yta.
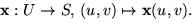 Härled en differentialekvation för u(t) och v(t), sådan
att
Härled en differentialekvation för u(t) och v(t), sådan
att 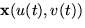 är en geodet på S om ekvationen satisfieras.
är en geodet på S om ekvationen satisfieras.
