Kommentarer till 2.2 och 2.3

Sidan 52: Stryk de två sista raderna i punkt 2 av definition 1.

Sidan 64: Rad 4 i beviset. Att dh_r är icke-singulär (inverterbar) kräver ett argument: Antag t.ex. att den lokala grafparametiseringen är $\mathbf y:V\rightarrow W,\,\mathbf y(u,v)=(u,v,f(u,v)),$ där $f:V\rightarrow \mathbb R$ är glatt. Detta tvingar $\mathbf x$ att ha formen $\mathbf x(u,v)=(x(u,v),y(u,v),f(x(u,v),y(u,v)))$ när $(u,v)\in N$. Vi kan se detta som sammansättningen av $N\rightarrow V,\,(u,v)\mapsto (x(u,v),y(u,v))$ följd av $\mathbf y:V\rightarrow W$.Jakobis matris blir då med hjälp av kedjeregeln

$$\left( \begin{array} {rrr} 1&0\\ 0&1\\ f'_{u}&f'_{v}\end{... ...ray} {rrr} x'_{u}&x'_{v}\\ y'_{u}&y'_{v}\\ \end{array}\right)$$

Eftersom $\mathbf x$ är en lokal parametrisering är denna linjära avbildning injektiv. Den högra linjära avbildningen är därför injektiv och därmed en bijektion eftersom den representeras av en kvadratisk matris. Men detta är precis Jakobis matris för h.

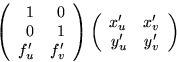
Sidan 72: Överst på sidan är det inte tillräckligt att välja N som angivet. Man ska använda kontinuiteten hos h för att välja N så att $h(N)\subseteq M_{0},$ där M₀ är diffeomorf med M via F.

På föreläsningarna ges ett alternativt bevis till proposition 1 på sidan 70.

Sidan 74: I exempel 3 är det bäst att välja $\mathbf x_{2}$ som en grafparametrisering så att $\mathbf x_{2}^{-1}\phi=\pi\phi,$ där $\pi$ är projektion på ett plan innehållande två av koordinataxlarna.