Det kontinuerliga fallet

Vi går nu raskt vidare och introducerar en innerprodukt för funktioner. Vi byter ut $\Re^n$ mot mängden av två gånger kontinuerligt deriverbara funktioner som uppfyller randvillkoren (noll i ändpunkterna). Den vanliga innerprodukten för vektorer, som är en summa, övergår i en integral:

$$(f, g)=\int_0^1f(t)g(t)dt$$

Vi ser att $(f,g)$ uppfyller villkoren på en innerprodukt.

Vi återvänder nu till differentialekvationen, $-u''=f$. Om vi inför operatornotation kan vi skriva $-u''={\cal A} u$. ${\cal A}$ är en operator (avbildning) som givet en funktion $u$ ger oss andraderivatan med ombytt tecken. Vårt problem kan då skrivas:

$${\cal A}u=f$$

Jämför likheten med ett linjärt ekvationssystem ${\bf A}{\bf u}={\bf f}$. En symmetrisk operator borde nu, i analogi med matrisfallet, uppfylla $(f,{\cal A}g)=({\cal A}f, g)$ för alla $f$ och $g$ som uppfyller randvillkoren.

Vår operator är symmetrisk och för att visa det utnyttjar vi partialintegration:

$$\left\{ \begin{array}{lllll} (f,{\cal A}g)&=\int_0^1f(t)(-g'... ...\int_0^1-f'(t)g'(t)dt&=\int_0^1f'(t)g'(t)dt \end{array}\right.$$

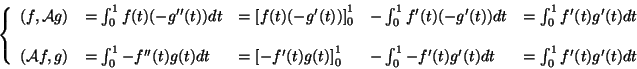
Kvantiteterna inom $\left[\ \ \right]_0^1$ blir noll på grund av randvillkoren. Operatorn är också positivt definit ty:

$$(f,{\cal A}f)=\int_0^1f(t)(-f''(t))dt=\left[f(t)(-f'(t))\right]_0^1- \int_0^1f'(t)(-f'(t))dt= \int_0^1(f'(t))^2dt>0$$

ty om $f$ är skild från nollfunktionen blir även $f'$ det.

När vi löser problemet numeriskt diskretiserar vi operatorn och får ett matrisproblem: ${\bf A}{\bf u}={\bf f}$. Det verkar då kanske rimligt att matrisproblemet ``ärver'' några av det kontinuerliga problemets egenskaper så att ${\bf A}$ blir symmetrisk och positivt definit.