System av ickelinjära ekvationer

Syftet med denna laboration är att Du lära Dig att ställa upp Newtons metod för ett system av ekvationer.
 
"Vi har en mottagare (på en robot) som kan avläsa avstånden till tre fixa sändare. Vi känner sändarnas positioner, och söker mottagarens position i rummet (tre koordinater)."

Antag först att allt mäts exakt. Formulera det system av tre ekvationer som vi måste lösa för att bestämma mottagarens position. Vad kan vi säga om lösningens entydighet (antag att sändarna sitter på olika ställen i rummet)? Vilka olika antal lösningar kan existera (kan det finnas en, två, tre, ..., oändligt många lösningar)?

I en verklig situation mäter vi inte exakt, det kan då vara så att det systemet saknar lösning. Det är därför rimligt att formulera problemet som ett ickelinjärt minstakvadratproblem istället. Eftersom Du har tränat på denna problemtyp i en annan laboration, så vi behåller systemet av tre ickelinjära ekvationer.

Skriv ett Matlabprogram som bestämmer mottagarens position med hjälp av ekvationerna från föregående övning och med hjälp av Newtons metod. Ditt program skall angripa de ursprungliga ekvationerna (du skall alltså inte lösa ut några variabler för hand; syftet är ju att träna på Newtons metod). Testa på data nedan och skriv ut p(k) i varje iteration (om p är den sökta positionen)! Spara lösningarna och antalet iterationer. Säg något lämpligt om vad de olika startpunkterna ger för uppförande. Skapa Jacobianen genom att derivera för hand, använd inte Matlabs jacobian-kommando.

Lite mätdata: Sändarnas positioner (klipp och klistra):

x = [ 1.23,  0.12, -0.22]';   % x-koordinaterna för sändarna
y = [ 0.01,  0.98,  0.02]';   % y-koordinaterna för sändarna
z = [-0.11, -0.12,  1.76]';   % z-koordinaterna för sändarna
r = [ 1.22,  0.98,  1.52]';   % avstånden mellan sändare och mottagare

Testa följande tre startvektorer (p(1) = den sökta x-koordinaten, p(2) och p(3) är y- och z-koordinater) :

p = zeros(3, 1);
p = ones(3, 1),
p = [3.407007110432360e-01
     3.907070706849901e-01
     4.758069306448354e-01];

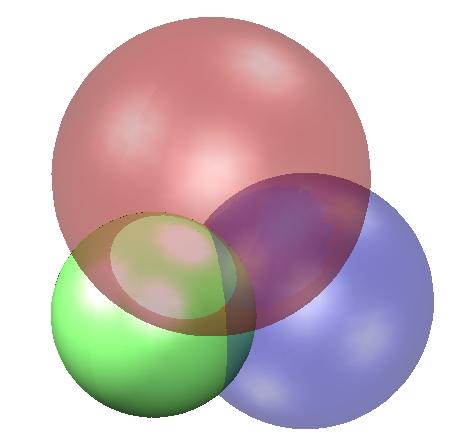
Om man kan Matlab (och använder belysning (tre lampor i detta fall), shading och transparens) kan man göra följande grafiska framställning av vårt problem: