Kvadratur och interpolation
Matlabs quadl är en
bra rutin som även kan hantera enklare
ändpunkts-singulariteter. Om singulariteten blir för uttalad
ger quadl ett
felmeddelande och svaret blir mindre bra. Så här kan det se
ut (jag har tagit bort varningen för nolldivision). Toleransen
är 1e-6 absolut.
>> fel = quadl(@(x) 1 ./
x.^0.7,
0, 1) - 1 / 0.3, % 1 / 0.3 är integralens exakta värde
fel = -6.1687e-06
% analogt i följande exempel
>> fel = quadl(@(x) 1 ./
x.^0.8,
0, 1) - 1 / 0.2
Warning: Minimum step size reached; singularity possible.
fel = -7.9354e-04
>> fel = quadl(@(x) 1 ./
x.^0.9,
0, 1) - 1 / 0.1
Warning: Minimum step size reached; singularity possible.
fel = -1.2600e-01
>> fel = quadl(@(x) 1 ./
x.^0.99, 0, 1) - 1 / 0.01
Warning: Minimum step size
reached; singularity possible.
fel = -6.4572e+01
För att klara av svåra fall kan man
använda variabelsubstitution eller partiell integration för
att bli av med singulariteten och få en snäll integrand som quadl kan hantera. I
följande uppgift får du träna på denna teknik.
Integrationsintervallet är [0, 1] i samtliga tre fall.
|

|
a) Använd partiell
integration följd av quadl
för att approximera den bestämda integralen av cos(x) /
x^0.9.
b) Använd variabelsubstitution följd av quadl för att approximera
den bestämda integralen av cos(x) / x^0.9. Ledning: testa
ansatsen t = x^p där p är ett
reellt tal.
c) Frivillig:
Använd variabelsubstitution följd av quadl för att approximera
den bestämda integralen av log(x) / (x^0.85 + x^0.9 +
x^0.95). Ledning: testa ansatsen t = x^p där p är ett
reellt tal.
|
|

|
Frivillig:
Kör (och studera) följande
Matlabprogram. Titta på
värdena och plotten. Förklara vad som händer.
Ledning: Hur lurar men en kvadraturmetod (vilken som helst)? Vikter och
abscissor är givna (och fixa).
Skriv ett program för Simpson formel och beräkna en
approximation av integralens värde.
|
Länkarna i det första stycket behöver du bara läsa
om intresse föreligger.
I följande uppgift kommer du att ta fram formen på ett bord.
Det är en typ av problem som jag har haft flera gånger.
Under de senaste åren har vi tagit fram ett bord som haft formen
av en superellips, ett mellanting mellan en ellips och en rektangel.
Formen,
som
har använts för fontäner och andra arkitektoniska
skapelser,
var
ett påfund av den danske mångsysslaren
Piet Hein,
en länk
till
(en del av en utmärkt matematisk uppslagsbok), slutligen Wikipedias
artikel. Här kan Du se
ett
bord, Supercirkel av Bruno Mathsson
& Piet
Hein.
Eftersom som jag har lagt till ovanstående två
övningar i år har jag förenklat designen av bordet. I
år kommer du att bestämma utseendet på ett bord som
har formen av en epicykloid.
Vi kommer att generalisera bilderna från länken till
vänster, man talar om shortened eller lengthened epicykloid
(kanske förkortad, förlängd på svenska). Här
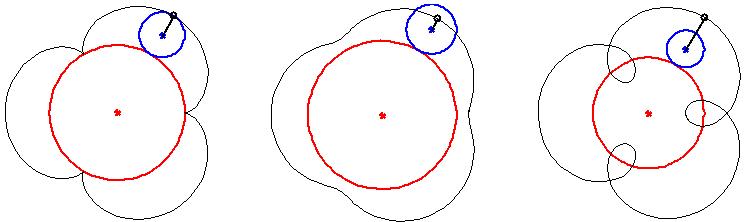
är tre epicykloider (de tre svarta kurvorna).
Den blå cirkeln rullar utmed den röda, utan att slira. Den
svarta ringens väg genererar kurvan. I nästa bild har den
svarta punkten flyttats in utmed den blå cirkelns radie, r.
Ringen befinner sig på avståndet 0.5 r från den
blå cirkelns centrum (shortened). I den tredje bilden har ringen
flyttats ut och befinner sig på avståndet 2 r från
blå cirkelns centrum (lengthened). Låt q vara graden av
förkortning eller förlängning, så i bilderna
är q = 1, q = 0.5 respektive q = 2. De tre bilderna är inte ritade i samma skala.
Om R är radien i den röda cirkeln så har kurvorna ovan
parameterframställningen:
R = 0.5
r = R /
3 (3 =
antalet utbuktningar)
c = (R + r) / r (= 3 + 1 = 4)
x(t) = c * r * cos(t) - q
* r
* cos(c * t)
y(t) = c * r * sin(t) - q
* r
* sin(c * t) då 0 <= t <= 2 pi
|

|
Vi råkar ha en tjusig,
4.25 m lång, kantlist
till bordet. Använd parameterframställningen ovan och
bestäm q så att epicykloidens omkrets blir 4.25 m.
Rita också upp formen på det resulterande bordet (glöm
inte axis equal, annars
får bordet fel form).
Ledning: Låt om(q)
vara bordets omkrets (epicykloidens kurvlängd) som funktion av q.
Då består problemet i att lösa ekvationen om(q) =
4.25. Använd fsolve
för att lösa ekvationen där du använder quadl för att beräkna
kurvlängden.
|
Sist en liten övning som visar på för- och nackdelar
med olika interpolationsförfaranden. Vi vill jämföra linjär
interpolation, splineinterpolation och så kallad "shape-preserving"
kubisk Hermiteinterpolation för två dataserier. Shape-preserving
innebär att om data är monotont (växande/avtagande på ett delintervall)
så är även interpolanten detta. En vanlig kubisk spline behöver inte
alls vara shape-preserving.
De två dataserierna, (t(k), y1(k)), k = 1, ...,, 8, respektive (t(k), y2(k)), k = 1, ...,, 8, skapar du så här:
t = linspace(-2, 3, 8)';
y1 = exp(-t.^2);
y2 = [-1 -1 -1 -1 1 1 1 1]';
I den första dataserien har du en underliggande funktion, exp(-t^2), att jämföra med när du studerar för- och nackdelar med de olika metoderna.
|

|
Använd Matlabrutinen interp1
för att testa de tre interpolationsmetoderna. Skapa ett plotfönster
vardera för de två dataserierna. I varje plotfönster skall
datapunkterna och de tre interpolaterna ritas ut.
Datapunkterna skall ritas med ringar och interpolaterna skall ritas som
kurvor på ett finare grid (använd 100 punkter). Använd slutligen legend-funktionen.
I
den första dataserien vet du vilken funktion vi försöker approximera.
Räkna ut maximala avvikelsen (på det finare gridet) för varje
interpolant.
Slutligen: drag slutsatser och analysera dina resultat"
|

![]()