Ett exempel på hur man använder lsqnonlin
Antag att vi har mätt upp utslag hos en partikel som utför en dämpad harmonisk svängningsrörelse. Vår modell är y = a exp(d t) cos(w t). y är utslaget (avvikelsen från jämviktsläget) hos partikeln och t är tiden. Modellen har tre parametrar, a, d och w, som vi vill bestämma. a står för amplituden, d för dämpningen och w för vinkelfrekvensen.
Vi har en uppsättning mätpunkter (tk, yk),
k = 1, ..., n och vill anpassa modellen till dessa mätvärden.
Funktionen lsqnonlin försöker minimera
följande kvadratsumma:
[y1 - a exp(d t1) cos(w t1)]2 + [y2 - a exp(d t2) cos(w t2)]2 + ... + [yn - a exp(d tn) cos(w tn)]2
med avseende på de tre parametrarna a, d och w. För att använda
lsqnonlin måste vi tillhandahålla en funktion, kalla
den residual, som räknar ut residualvektorn (rutinen
skall alltså inte räkna ut kvadratsumman) givet de aktuella
uppskattningarna av parametrarna. lsqnonlin prövar sig
fram med olika parametervärden och vill, för varje uppsättning,
få tillbaks residualvektorn. Funktionen residual tar bara
en inparameter, nämligen en vektor som innehåller de aktuella
uppskattningarna av parametrarna i modellen, så vi måste alltså
förpacka a, d och w i en vektor. Det är vanligt att numerisk
programvara utformas med standardiserade parameterlistor på detta
sätt (man har alltså inte olika antal inparametrar beroende
på antalet parametrar i modellen).
Observera att alla variabler i funktionen är lokala till funktion (så att om jag har definierat t- och y-värden enbart i funktionen, så kommer man inte åt dessa variabler "utifrån" och vice versa). Detta problem (att ge både huvudprogram och funktion tillgång till t- och y-värden) kan lösas på minst tre olika sätt:
lsqnonlin har tänkt på detta
problem och har gjort det möjligt att skicka med extra variabler
(help lsqnonlin för detaljer)global (global-deklarationen måste
finnas både i funktionen och i "huvudprogrammet").
I följande exempel har jag utnyttjat global eftersom det är standardlösningen. Så här ser t- respektive y-värdena ut:
t y 0 1.3787e+01 1.0871e+00 2.4637e+00 2.1971e+00 -8.2296e+00 3.0095e+00 -7.0862e+00 4.3971e+00 7.2126e+00 5.2744e+00 7.8584e+00 6.2714e+00 1.1796e+00 7.3574e+00 -5.4583e+00 8.3811e+00 -2.5818e+00 9.1610e+00 8.9438e-01 1.0589e+01 4.4598e+00 1.1582e+01 3.0895e-02 1.2956e+01 -2.9151e+00 1.3504e+01 -1.4731e+00 1.5205e+01 3.2932e+00 1.6419e+01 8.1525e-01
och jag förutsätter att vektorn t innehåller
t-värdena och att vektorn y innehåller y-värdena.
function r = residual(params) % Vi använder global för att få tillgång till mätdata. % Denna deklaration måste också finnas i huvudprogrammet. global t y % Här packar vi upp params. Detta är inte nödvändigt % vi kan givetvis referera till params(1) etc. direkt. a = params(1); % Aktuell uppskattning av amplituden d = params(2); % av dämpfaktorn w = params(3); % och av vinkelfrekvensen % Här beräknar vi residualen och tilldelar % den till resultatvariabeln r. % OBS: rutinen skall returnera en vektor av residualer % och INTE kvadrater av residualer eller en kvadratsumma. r = y - a * exp(d * t) .* cos(w * t);
Jag har också skapat en fil main.m där jag anropar
lsqnonlin plottar mätdata och modellen. Den svåraste
delen i main.m är att hitta på bra startvärden
(gissningar). Vi har ju ett ickelinjärt problem. Dåliga
startvärden kan medföra att vi inte får konvergens eller
att vi hamnar i en minpunkt med större fel i anpassningen. Även
om det kan konvergera med dåliga startvärden så brukar det
gå snabbare om man startar nära minimum.
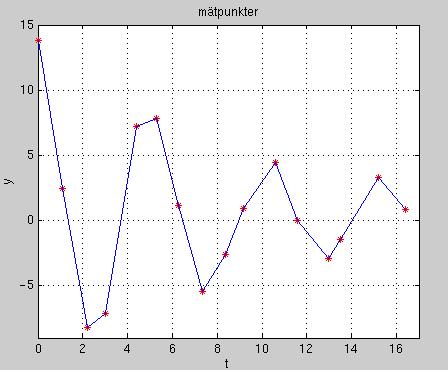
Så här ser mätpunkterna ut (röda *) där jag har förbundit punkterna med räta linjesegment.

Som gissning på amplituden kan vi ta y(1) eftersom
t(1) = 0.Från figuren ser jag att kurvan svänger
ungefär tre hela perioder mellan första och näst sista
mätvärdet. Jag uppskattar därför w till 6 pi / t(end-1).
(end är en funktion som står för indexet för sista
elementet). Det är svårare att uppskatta dämpningen. Ett
sätt är att betrakta de värden vi gissat för amplitud
och vinkelfrekvens som givna, sedan logaritmera och lösa det linjära
minstakvadratproblemet. Man får se till att bara plocka ut de
tidsvärden där argumenten till log-funktionen blir positiva. Detta
ger oss approximationen -8.7622e-02.
Ett enklare sätt är att välja en tidpunkt tk och lösa ut dämpningen ur sambandet yk = a exp(d tk) cos(w tk), där vi betraktar de gissade värdena på amplitud och vinkelfrekvens som givna. Man skall inte ta ett tidsvärde där yk är för nära noll eftersom man kan anta att mätbruset är stort jämfört med själva y-värdet. Jag har, lite godtyckligt, valt (t5, y5).
Här kommer main.m (notera att jag har samma ordning på
parametrarna i startvektorn som jag har i funktionen residual):
% En matchande global-deklaration.
global t y % Här ger jag t och y värden. Jag har inte skrivit ut alla värdena. t = [ 0 1.0871 ... ]'; y = [13.787 24.637 ... ]'; % Bestäm startvärden, gissningar på parametrarna. a_gissning = y(1) w_gissning = 6 * pi / t(end - 1) d_gissning = log(y(5) / (a_gissning * cos(w_gissning * t(5)))) / t(5) % Stoppa in gissningarna på rätt platser i startvektorn. start_gissning = [a_gissning; d_gissning; w_gissning]; % Anropa lsqnonlin. I params hamnar de optimala värdena, % förutsatt att allt fungerar som det ska. params = lsqnonlin(@residual, start_gissning) figure(1) hold off plot(t, y, 'r*') % plotta mätdata xlabel('tid') ylabel('y') title('Mätdata och anpassning') hold on % Skapa en t-vektor, med fin uppdelning, för att plotta % modellen som ju beror kontinuerligt av t. t_fin = linspace(t(1), t(end)); plot(t_fin, params(1) * exp(params(2) * t_fin) .* cos(params(3) * t_fin)) grid on
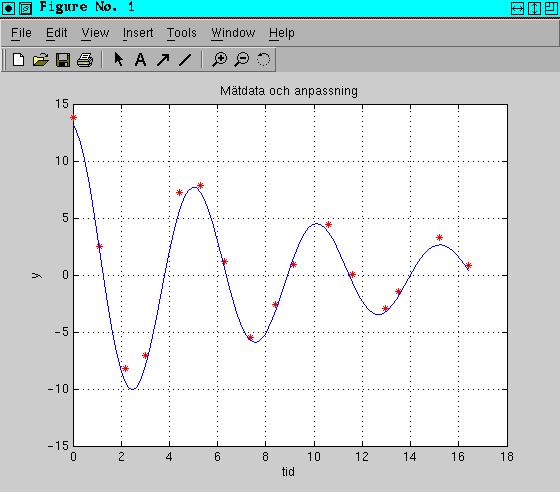
Här är körningen (något redigerad). Vi kan notera att jag gissade väldigt bra i detta fall (snälla mätvärden).
>> main a_gissning = 1.3787e+01 w_gissning = 1.2397e+00 d_gissning = -1.9390e-01 Optimization terminated successfully: Relative function value changing by less than OPTIONS.TolFun params = 1.3099e+01 % optimala a -1.0447e-01 % d 1.2330e+00 % w
Så här blev plotten: