Lab2a

Mer om loopar, vektorer

Laborationen ger träning på grundläggande programmering, repetitionssatser, villkorssatser, vektorer samt grafik.

Introduktion:
I mekanik-kursen får du se (har sett) hur man löser rörelse-ekvationerna för två respektive för tre kroppar (tvåkropparsproblemet, trekropparsproblemet). För mer än tre partiklar kan man lösa rörelse-ekvationerna approximativt med hjälp av numeriska metoder. Något om detta kommer i kursen i numerisk analys som kommer efter Matlab-kursen. När man har många partiklar, t.ex. när man vill simulera hur stjärnor formar galaxer krävs speciella metoder och parallelldatorer.

Om man har väldigt många partiklar, molekyler i en gas t.ex, är det inte möjligt att lösa rörelse-ekvationerna på vanligt sätt. Istället kan man använda statistiska metoder, statistisk fysik (kommer under fysikprogrammets femte termin). Man beskriver då inte de enstaka molekylernas rörelser utan sammanfattar alla molekylernas rörelser i makroskopiska egenskaper. I kursen statistisk fysik kommer du t.ex. att se att temperaturen, T, hos en (ideal) gas kan skrivas E = k T / 2 där E är medelvärdet av gaspartiklarnas kinetiska energier och k är Boltzmanns konstant.

I denna lab kommer du att leka med dessa begrepp, fast utan att göra någon fysik eller matematik, genom att simulera diffusion av gas. I figuren nedan är en tvådimensionell modell av en gasbehållare. Behållaren är 2L (L = lämplig längdenhet) bred och 1L hög. Gaspartiklarna är de svarta prickarna. I behållaren finns en barriär, den röda rektangeln. Utsträckning på barriären framgår av figuren (mellan 0.9L och 1.1L i x-led och mellan 0L och 0.9L i höjdled). Gaspartiklarna kan inte passera genom barriären utan bara genom den lilla öppningen ovanför barriären.

Vi tänker oss att gaspartiklarna initialt finns i behållarens vänstra del, som i bilden. Partiklarna rör sig sedan slumpmässigt (vi löser alltså inte några rörelse-ekvationer och tar t.ex. inte hänsyn till att partiklar stöter ihop) och vi vill animera detta förlopp genom att visa en sekvens av bilder i en loop. Under en iteration i loopen uppdaterar vi partiklarnas positioner, partiklarna kommer då att se ut att röra på sig. Nästa bild visar hur situationen kan se ut efter 1000 iterationer. Aktuellt antal iterationer svarar alltså mot den tid som gått.

Efter 1000 iterationer

Vi noterar att några partiklar har tagit sig in i den högra delen av behållaren och några är på väg (ligger ovanför barriären).

Antag att (x, y) är aktuell position hos en partikel. Den nya positionen låter vi vara (x + dx, y + dy) där dx = slumptal, dy = slumptal, där slumptalen (olika) är likformigt fördelade slumptal i ett lämpligt intervall, (-d, d), d > 0. Med likformigt fördelade menas att varje tal i intervallet (-d, d) är lika sannolikt. Man kan argumentera för att normalfördelade slumptal är ett mer naturligt val, men dels har du har ju inte läst kursen i matematisk statistik än och dels underlättar det programmeringen om vi vet att en partikel inte kan röra sig godtyckligt långt under en iteration (den kan inte passera rakt igenom barriären med lämpligt val av parametern d). Man väljer d så att man får en rimligt kontinuerlig animation och så att, som sagt, ingen partikel kan passera igenom barriären i en iteration. Använd Matlab-funktionen rand för att producera slumptal. Observera att man får generera nya slumptal för varje partikel i varje iteration.

Partiklar kommer att stöta emot behållarens samt barriärens väggar. Vi simulerar det på följande vis. Om (x + dx, y + dy) ligger utanför behållaren eller inuti barriären så placerar vi partikeln på väggen. Säg att (x + dx, y + dy) = (-0.21, 0.74). Vi låter då partikelns position vara (0, 0.74) (analogt i övriga fall).

Överst i figurfönstret skriver vi ut det aktuella iterations-numret (1000 i andra figuren) som alltså räknas upp hela tiden. Matlab-funktionerna num2str samt title är då användbara.

När animationen är färdig skall ytterligare ett fönster öppnas och i detta skall relativa andelen partiklar i den vänstra halvan av behållaren ritas ut som funktion av iterationerna (relativa andelen är aktuellt antal partiklar delat med ursprungsantalet). Det kan se ut så här:

Man skulle kunna fundera över vilken typ av funktion som detta är (bortse från hackigheten), men det är då rimligt att använda partiella differentialekvationer, så vi avstår från närmare analys. Så här kan det dock se ut med många partiklar (den svarta kurvan) och en, av mig, anpassad deriverbar funktion, den röda kurvan.

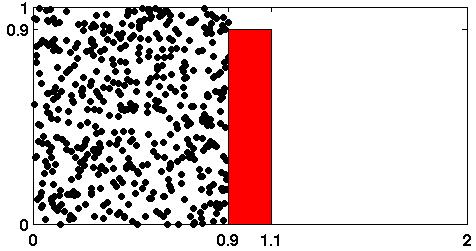
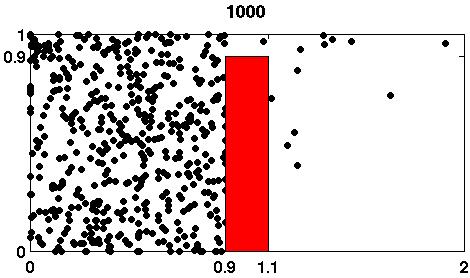
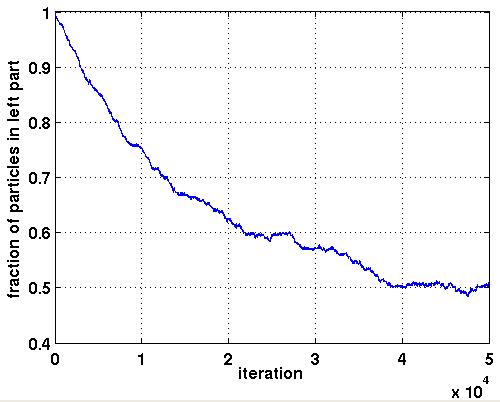
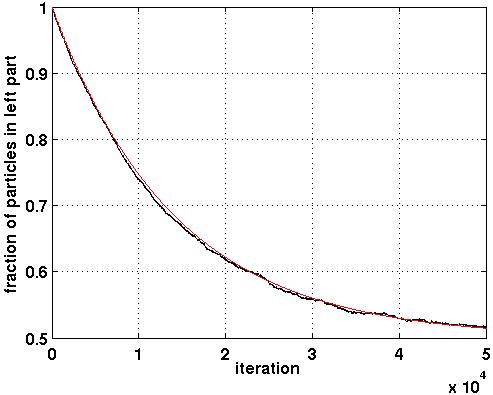
Skriv en Matlabfunktion, diff_anim, enligt ovanstående idéer. diff_anim skall anropas med två parametrar, diff_anim(no_of_part, no_of_iterations). no_of_part är antalet partiklar och no_of_iterations är antalet iterationer. Partiklarnas ursprungspositioner skall slumpas ut i området 0 <= x <= 0.9, 0 <= y <= 1.

Om no_of_part eller no_of_iterations har ett orimligt värde så skall rutinen ge ett felmeddelande (använd Matlab-funktionen error) och inga fönster skall öppnas.

Här några tips om du åstadkommer animeringen. Barriären ritar du med fill-kommandot.

Frivilligt: om du har tid och intresse kan du simulera några andra fall.

Vi kan simulera gravitation genom att använda ett osymmetriskt intervall för dy. Om det är mindre sannolikt att partikeln rör sig i positiv y-riktning så kommer partiklarna att sjunka ner. Den vänstra halvan av behållaren fungerar då som en potentialgrop.
En lite annan tolkning av detta är en kastrull med kokande vatten. De flesta partiklarna är bundna till vätskan, men en del får tillräcklig energi för att lämna vattenytan och rör sig uppåt.

Man kan lämpligen ändra funktionen så att den anropas diff_anim(no_of_part, no_of_iterations, dy_limits), där dy_limits är en vektor, med två element, som definierar slumptalsintervallet. Man kan givetvis införa en dx_limits-vektor också, då kan man simulera att partiklarna driver åt höger eller vänster.
Antag att barriären går ända upp till behållarens övre kant, men att barriären är genomsläpplig (och inte lika tjock som den röda). Med viss sannolikhet kan en partikel passera igenom barriären. Detta kan användas för att göra en modell av osmos, där barriären kan svara mot ett cellmembran.

Hur man testar sitt program:

Program testing can be used to show the presence of bugs, but never to show their absence!
Edsger Dijkstra

A bug-free program is an abstract. theoretical concept.
Dennie Van Tassel

All sufficiently complex programs have bugs.
Anonymous

An effective way to test code is to exercise it at its natural boundaries.
Brian Kernighan

Normalt kan vi inte vara helt säkra på att ett program fungerar i alla detaljer. De flesta program fungerar nog under normal drift, men kan nog räkna fel vid ovanliga indata. Här några skräckhistorier: Collection of Software Bugs, Software horror stories. Programmet i denna lab är dock tämligen enkelt och vi kan genom omsorgsfull programmering och testning övertyga oss om att de (nog) är bugfria. Absolut säkerhet uppnår vi aldrig. Även om vårt program är korrekt, så körs det ju i Matlab (som är ett stort komplicerat program; jag har själv rapporterat flera buggar), på en mycket komplex apparat (en dator) som styrs av Linux, ännu ett stort programsystem.

När man testar sitt program bör man ha med några typiska fall, men även undantagsfall (som Brian Kernighan förordar). Man gör nog ofta rätt på normalfallet, men tänker sig inte för vid ovanliga fall. Slumpdata är inte så användbara som skulle kunna tro, eftersom de brukar vara rätt så snälla. Om man t.ex. vill testa en rutin för att beräkna egenvärden till en matris, så ger slumpdata snälla matriser. Svåra problem har t.ex. multipla egenvärden, ett undantagsfall.

Se till exempel till att ditt program fungerar med en partikel eller en iteration.