
 |
Varför är
ovanstående resonemang korrekt? |
 |
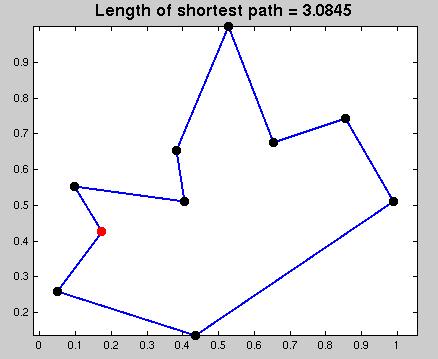
Skriv ett rekursivt Matlabprogram som
räknar ut och ritar ut kortaste vägen enligt
specifikationerna ovan. Testa åtminstone på följande
data och bifoga längden på
kortaste vägen och bilder
med den kortaste vägen utritad. Se exempelbilden nedan. Testfall. Indata är (x1, y1), (x2, y2) respektive (x3, y3). Börja med att testa på något enklare! phi = linspace(0, 2 * pi, 13)'; phi = phi(1:12); x1 = cos(phi); y1 = sin(phi); x2 = [2 3 8 1 3 0 4 2 7 5 9 6 5]'; y2 = [3 3 0 2 6 6 9 2 8 6 0 4 4]'; phi = linspace(0, 4 * pi, 13)'; r = (1:13)'; x3 = r .* cos(phi); y3 = r .* sin(phi); Jag har fått frågor om körtider för dessa tre fall. Med greedy-startgissningarna tar mitt program 0.2s, 12.8s respektive 97.4s. |