1. a)
2. a)
3. Nej! Reflektion?
4.
5. Manuell räkning ger (minsta kvadrat) lösningarna
7.
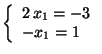 b)
b)
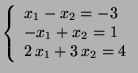 c)
c)
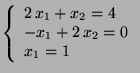 d)
d)
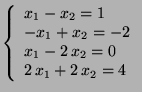
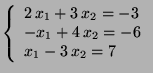 b)
b)
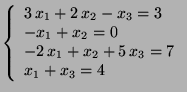 c) Beräkna i fallet 2a resp 2b ``minsta kvadratfelet'' i lösningen, dvs
c) Beräkna i fallet 2a resp 2b ``minsta kvadratfelet'' i lösningen, dvs 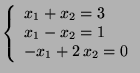 . Beräkna felet
. Beräkna felet 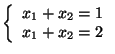 . Jämför felet
. Jämför felet
Svar:
1.
a) ![]() b)
b)
![]() c)
c)
![]() d)
d)
![]()
2.
a)
![]() b)
b)
![]() c)
c) ![]() resp
resp ![]()
3.
Nej! Reflektion?
4.
![]() . Fel
. Fel ![]() . Även överbestämda system kan ha exakt lösning!
. Även överbestämda system kan ha exakt lösning!
5.
Manuell räkning ger (minsta kvadrat) lösningarna
![]() . Matlabs
. Matlabs
![]() ger
Inf, eftersom
ger
Inf, eftersom ![]() singulär. Med en ekvation till ger matlabs
singulär. Med en ekvation till ger matlabs
![]() minsta kvadratlösningen. Ekvationssystemet
minsta kvadratlösningen. Ekvationssystemet
![]() löser matlab med
löser matlab med
![]() (motsvarande
(motsvarande ![]() med en varning). Reflektion: Kan finnas flera (lika bra/dåliga) minsta kvadrat ``lösningar''.
med en varning). Reflektion: Kan finnas flera (lika bra/dåliga) minsta kvadrat ``lösningar''.
7.
![]() och
och ![]() .
.