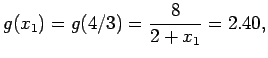Next: Implementation i Matlab
Up: Studio 3
Previous: while-Loopar
Fixpunktsiteration är ett, vanligtvis ineffektivt, sätt att lösa
ekvationer på. Iden är emellertid enkel. Antag att vi vill lösa
andragradsekvationen
Vi börjar då med att skriva om ekvationen så att vi få r
ett 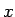 i vänsterledet, genom att dividera med
i vänsterledet, genom att dividera med 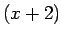
Ekvationen har nu formen
där
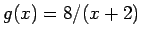 . Om
. Om 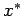 betecknar den exakta lösningen till
betecknar den exakta lösningen till
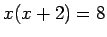 har vi tydligen
har vi tydligen
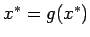 .
.
Nästa steg är att gissa en approximation till 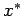 , t.ex.
, t.ex. 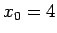 och evaluera
och evaluera
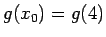 . Vi får då
. Vi får då
Förhoppningen är nu att detta värde, som vi fortsättningsvis kallar
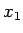 skall vara en bättre approximation till
skall vara en bättre approximation till 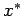 än
än 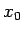 . Det
finns inget som styrker att detta antagande är sant just nu, men om
det är så, så borde ju
. Det
finns inget som styrker att detta antagande är sant just nu, men om
det är så, så borde ju
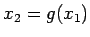 vara en ännu bättre approximation
till
vara en ännu bättre approximation
till 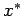 . Alltså, låt oss också räkna ut
. Alltså, låt oss också räkna ut 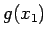 . Vi får
. Vi får
som vi kallar 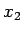 , och tror är den bästa approximation till
, och tror är den bästa approximation till 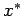 som vi hittils räknat ut.
som vi hittils räknat ut.
Håller vi nu på så här genereras en sekvens med tal,
som vi hoppas konvergerar mot 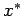 om
om 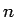 är stort. Detta
kallas fixpunktsiteration.
är stort. Detta
kallas fixpunktsiteration.



Next: Implementation i Matlab
Up: Studio 3
Previous: while-Loopar
Fredrik Bengzon
2004-08-24
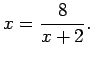
![]() , t.ex.
, t.ex. ![]() och evaluera
och evaluera
![]() . Vi får då
. Vi får då