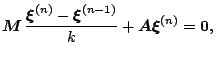Next: Computer Assignment
Up: Time Dependent Problems
Previous: Space Discretization
By applying finite elements to (1) we have derived the
semi-discrete problem
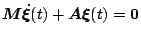 , which we now must solve. To do so we introduce a
partition
, which we now must solve. To do so we introduce a
partition
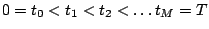 of the time interval
of the time interval
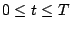 into
into 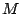 subintervals of equal length
subintervals of equal length 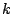 and
replace the time derivative
and
replace the time derivative
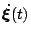 by a difference
quotient viz.,
by a difference
quotient viz.,
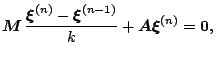 |
(13) |
where
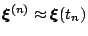 . Rearranging terms we
then have the iteration scheme
. Rearranging terms we
then have the iteration scheme
which is also known as the Backward Euler Method. There are
different choises of initial data
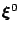 but the simplest is
to let
but the simplest is
to let
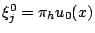 that is to use the linear interpolant
of
that is to use the linear interpolant
of 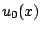 . Thus one starts from the initial data and successivly
compute solution approximations
. Thus one starts from the initial data and successivly
compute solution approximations
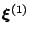 ,
,
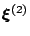 ,
, 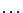 at times
at times 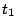 ,
, 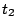 ,
, 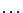 using the algorithm (14).
using the algorithm (14).
Mohammad Asadzadeh
2004-08-27
![]() , which we now must solve. To do so we introduce a
partition
, which we now must solve. To do so we introduce a
partition
![]() of the time interval
of the time interval
![]() into
into ![]() subintervals of equal length
subintervals of equal length ![]() and
replace the time derivative
and
replace the time derivative
![]() by a difference
quotient viz.,
by a difference
quotient viz.,