Grafik

Enkel grafik

Här följer exempel på hur man använder några få av Matlabs många plotrutiner.

Att plotta y = f(x)
Att plotta punkter
Mer än en kurva
Mer än ett fönster (eller flera axlar i ett fönster)
Att få korrekt axelskalning
Att plotta kurvor i rummet och planet
Att plotta polygoner i planet
Att plotta en funktionsyta, z = f(x, y)

Att plotta y = f(x)

>> x = linspace(0, 10); % 100 x-värden från 0 till 10. linspace(0, 10, 50) ger 50 värden
>> plot(x, exp(-0.1 * x) .* cos(x)) % plotta en heldragen kurva
>> grid on                % stödlinjer
>> xlabel('x')            % lite text utmed x-axeln
>> ylabel('y')        % y-axeln
>> title('En enkel kurva') % och en rubrik

Att plotta punkter
>> plot(x, y, 'o') % plottar punkterna (x(k), y(k)) med ringar
>> plot(x, y, 'r*') % plottar punkterna (x(k), y(k)) med röda *

Mer än en kurva
Det finns väsentligen två alternativ, det första är att plotta flera kurvor med ett plot-kommando:

>> plot(x, exp(-0.1 * x) .* cos(x), x, sin(x)) % två kurvor

>> plot(x, exp(-0.1 * x) .* cos(x), 'r-', x, sin(x), 'b--') % två kurvor, en röd heldragen och en blå streckad

Man kan också "hålla kvar" en plot med kommandot hold on. Om man kör sitt program flera gånger får man inte glömma att slå av hold-funktionen, med hold off, annars kommer man att accumulera fler och fler plottar i samma fönster. Jag utgår i följande exempel i från av vi inte har gett hold on-kommandot.

>> plot(x, exp(-0.1 * x) .* cos(x)) % plotta en kurva (plot rensar först fönstret)
>> hold on                           % håll kvar
>> plot(x, sin(x))                   % bygg på

>> hold off                          % slå av hold
>> plot(x, exp(-0.1 * x) .* cos(x), 'r-') % rensa och plotta sen kurvan
>> hold on                           % håll kvar
>> plot(x, sin(x), 'b--')            % bygg på

Mer än ett fönster (eller flera axlar i ett fönster)
figure skapar ett nytt fönster. Det senaste öppnade blir aktivt (där hamnar nästa plot). Man kan göra ett fönster aktivt genom att klicka på det. Alternativt kan man skriva t.ex. figure(2), där 2 är fönstrets nummer. Detta ser också till att fönstret lägger sig överst, så att man inte behöver leta efter det. Finns det inget fönster med nummer två, så skapas det.
Jag använder ofta följande kommando-sekvens.

figure(1) % aktivera fönster ett och lägg det överst
hold off   % slå av hold
plot(...   % ge lämpligt plotkommando
hold on    % håll kvar plotten
plot(...   % nytt plotkommando

Man kan också rita flera axlar (plottar) i ett fönster (man behöver inte ha alla kommandona på en rad). help subplot för detaljer.

>> figure(2)
>> x = linspace(1, 10);
>> subplot(221); plot(x, log(x));       axis equal; grid on    
>> subplot(222); semilogx(x, log(x));   axis equal; grid on
>> subplot(223); semilogy(x, exp(x));   grid on
>> subplot(224); loglog(2.^x, exp(x));  grid on

Att få korrekt axelskalning

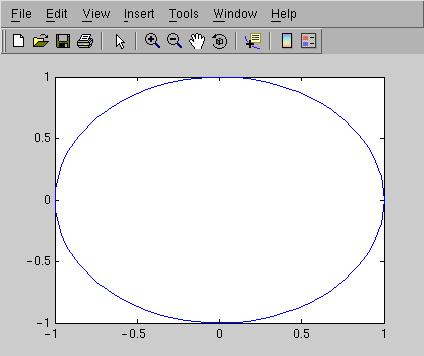
Följande kodsegment är tänkt att rita en cirkel:

>> f = linspace(0, 2 * pi); >> plot(cos(f), sin(f))

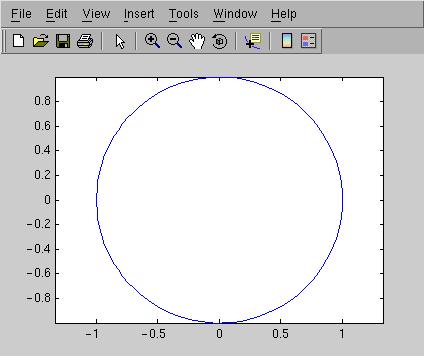
Den vänstra bilden visar resultatet. Cirkeln ser ut som en ellips eftersom Matlab försöker att utnyttja fönstret maximalt och fylla ut det. Om jag vill få en korrekt bild måste jag skala om axlarna. Om jag ger kommandot axis equal efter att ha plottat får jag bilden till höger. Observera att axis square inte gör samma sak (kommandot ger axlar som upptar lika många centimeter i x- och y-led).

Ellips Cirkel

Om spiralen, eller vad det nu är, fortfarande inte är korrekt skalad och du kör Linux, testa med att ändra skärmupplösning genom att ge kommandot xrandr -s 0 i ett terminalfönster (dvs. inte i Matlab).

Att plotta kurvor i rummet och planet
Om vektorerna x och y innehåller punkter på kurvan kommer plot(x, y) att förbinda punkterna (i ordning) med räta linjesegment och vi får en kurva i planet (som i exemplet ovan). Har vi också en z-vektor ger plot3(x, y, z) en kurva i rummet.
Här en rymdkurva som svänger likt en sinus-kurva i z-led och som går som en cirkel i x-y-planet.

>> f = linspace(0, 2 * pi);
>> plot3(cos(f), sin(f), sin(4 * f)) % fyra perioder
>> axis equal
>> grid on

Ökar vi antalet svängningar i z-led räcker kanske inte de 100 punkterna som linspace ger oss utan kurvan blir hackig, eftersom man ser de enskilda linjesegmenten.

>> plot3(cos(f), sin(f), sin(10 * f)) % blir hackigt vid min och max

>> f = linspace(0, 2 * pi, 200);       % be om 200 punkter
>> plot3(cos(f), sin(f), sin(10 * f)) % ger inga hack

Här några exempel till. Följande kommandosekvens ger ett Z, en sluten kurva, enligt bilden:

>> x = [1   0   0   0.1 0.2 0.7 0 0 1 1   0.9 0.8 0.2 1   1];
>> y = [1.4 1.4 1.1 1.1 1.2 1.2 0.3 0 0 0.3 0.3 0.2 0.2 1.2 1.4];
>> figure(1)
>> set(1, 'Color', 'w') % bakgrundsfärg = vit
>> plot(x, y, 'r', 'Linewidth', 3)
>> axis equal
>> axis off              % slå av axelgraderingen

Följande kod åstadkommer rymdkurvan nedan:

>> X = [x x x x]; % upprepa punkterna
>> Y = [y y y y];
>> Z = linspace(0, 1, length(X));
>> plot3(X, Y, Z, 'Linewidth', 2)
>> axis equal
>> axis off
>> view(25.5, 80) % placera bilden

Att plotta polygoner i planet
Vi kan använda det vanliga plot-kommandot för att rita randen på en polygon, så detta avsnitt visar hur man fyller en polygon med färg. När vi fyller polygoner behöver vi inte sluta randkurvan. Det räcker med att definiera hörnen (i ordning, med- eller moturs).

>> fill([0 1 1 0], [0 0 1 1], 'r') % en fylld, röd, enhetskvadrat

Numreringen är viktig, följande plot ger en fluga (till en kostym):

>> fill([0 1 1 0]', [0 1 0 1]', 'b')

Här ritar jag två polygoner med ett kommando (enhetskvadraten samt denna translaterad med vektorn (1, 1)). Kommandot är ett specialfall av fill(X, Y, 'r'). Först kolonnen i X samt första kolonnen i Y definierar hörnen i första polygonen. Andra kolonnen i X resp. Y definierar andra polygonen etc.

>> x = [0 1 1 0]'; % notera ', transponat
>> y = [0 0 1 1]';
>> fill([x x+1], [y y+1], 'r')

Om man inte vill ha några kantlinjer skriver man:

>> fill([x x+1],[y y+1], 'r', 'Edgecolor', 'None')

Vill vi ha gröna, breda kantlinjer skriver vi:

>> fill([x x+1], [y y+1], 'r', 'Edgecolor', 'g', 'Linewidth', 5)

Att plotta en funktionsyta, z = f(x, y)

Antag att vi vill rita punktmängden (ytan)

M = {(x, y, z): z = f(x, y), (x, y) tillhör D} där D = {(x, y): x_min <= x <= x_max, y_min <= y <= y_max}

så D är ett rektangulärt område i x-y-planet.

Ett sätt att göra detta i Matlab är att först bilda ett rutnät (grid) i mängden D. För att förstå hur detta fungerar, exekvera följande Matlabrad och inspektera X och Y.

[X, Y] = meshgrid(-1:0.5:1, 1:4)

Antag nu att matrisen F, innehåller funktionsvärdena, f(X(j, k), Y(j, k)). Kommandot

mesh(X, Y, F)

ritar då en approximation, i form av ett nät, av ytan. Ju bättre upplösning man har i rutnätet desto jämnare yta får man. Samtidigt tar matriserna mer plats och grafiken blir slöare (om man vill snurra på ytan till exempel). Tänk också på att om Du fördubblar antalet punkter i x- och y-led så innehåller matriserna fyra gånger så många element.

Matrisen F kan byggas upp med loopar, men ett snabbare och enklare sätt är att använda elementvisa operationer. Testa t.ex. följande rader:

x = linspace(-1, 1, 10); % Dålig upplösning y = linspace(0, 2, 10); [X, Y] = meshgrid(x, y); F = X.^2 .* Y; % Observera punkterna figure % Skapa nytt fönster mesh(X, Y, F) rotate3d % Slå på rotation figure % (kan klicka på rotationspilen också) surf(X, Y, F) % Ett annat sätt att rita ytan
shading interp % Jämna ut färgerna (löst uttryckt)
rotate3d

Regnbågsfärgen i ovanstående bild kan ändras (man kan ha en färg och lägga på belysning t.ex.) men vi tar inte upp detta i denna kurs.