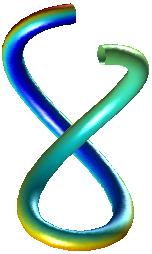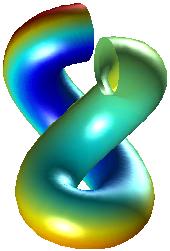Syftet med denna laboration är att Du skall få lite träning på rymdgeometri, parameterframställning, modellering, färg och belysningsmodeller. Uppgiften består i att skapa ett rör runt en kurva, c,  given i parameterform, c(s) = (x(s), y(s), z(s)), s = s_begin, s_end. En verklig användning av en sådan modul är till exempel att rita upp oljepipelines på Nordsjöns botten. Pipelinen definieras av en kurva och en radie. I den verkliga tillämpningen skall havets botten även ritas ut.

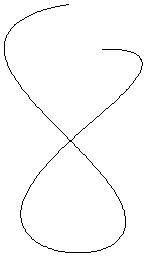
I bilden nedan visas en kurva längst till vänster och två rör (med olika diametrar) till höger:
 
 

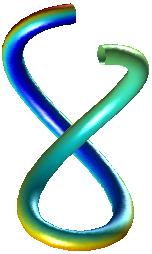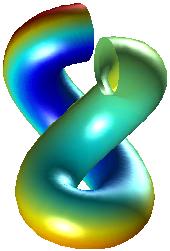Observera hur mycket enklare vi ser djupet i de två högra bilderna. Den första bilden är i princip omöjlig att tolka. Färgvalet är tämligen slumpartat i mitt exempel, men det är inget som hindrar att man har en mer enhetlig färg: ett grönt plaströr t.ex.:

Kurvans parameterframställning är i detta fall: (sin(s) cos(s),  0.2 s+sin(s) sin(s); 0.05 s+cos(s)) och parameterintervallet är [0, 2 pi].
Ditt program skall givetvis fungera för en godtycklig kurva.

Du kommer att använda två av Matlabs kommandon, fill3 resp. surf,  för att skapa röret. fill3 är ett kommando med vars hjälp man kan rita polygoner i rummet. Med surf kan man rita ytor som definierats av punkter på ytan (Matlab skapar själv en yta givet punkterna). Man kan skapa allmännare ytor med hjälp av fill3, men surf ger ett mer realistiskt resultat i denna laboration. Om Du planerar lite kommer Du att kunna använda nästan samma kod till båda uppgifterna.

Några tips om hur man använder fill3. Vi vill dela in kurvan i delintervall c(s), s = [s_begin, s₁], [s₁, s₂], ..., [s_n-2, s_n-1], [s_n-1, s_end]. Röret approximeras med ett rakt rör, uppbyggt av polygoner, i varje delintervall (se bilden nedan).

Längden på varje delintervall bestäms lämpligen med utgångspunkt från hur mycket kurvan kröker sig. Om kurvan nästan är rak kan man ha långa intervall och om kurvan har en tvär böj får man ha korta intervall (i böjen). Använder vi terminologi från ode-lösare och optimeringsalgoritmer ser vi att det är en adaptiv steglängdsalgoritm vi behöver. Om det aktuella värdet på parametern är s_k och nästa värde är s_k+1 säger vi att steglängden är s_k+1-s_k; mer om detta nedan. För tillfället (och i den första implementationen av programmet) använder vi fix steglängd (dvs. s ökas med lika mycket i varje steg).

Nu några ord om ett (av flera) sätt att skapa ett rörsegment. Låt t(s) vara kurvans tangent (vi antar att den alltid existerar; vi struntar i kurvor med spetsar t.ex.) och bilda planet som ortogonalt mot t(s) (dvs. ortogonalt mot kurvan för det givna parametervärdet s). Tänk Dig nu en cirkel i detta plan med radien r (rörets radie) och där kurvan går genom centrum. Bilda nu dessa plan och cirklar för s = s_k  och s = s_k+1. Vi vill nu förbinda cirklarna med en cylinderliknande yta. Vi gör det genom att dela in cirklarna i ett antal (m säg) lika stora segment och där vi markerar ändpunkten av varje segment med en punkt på cirkeln. (Jag använder följande språkbruk: ett rörsegment är en "rörbit" och ett segment är en del, en rektangel, av ett rörsegment.) Slutligen förbinder vi, med räta linjestycken, punkter parvis på de två cirklarna. Denna konstruktion definierar nu en uppsättning fyrhörningar. Ju fler segment vi använder desto bättre approximation av rörformen får vi. Om vi delar in cirkeln i t.ex. tre segment får vi trekantiga rör (ett Tobleronerör). Vi tänker oss att alla cirklar utmed kurvan indelas i lika många segment. Vi vill slippa vridna fyrhörningar vilket kräver viss eftertanke, som vi kommer att se. Om vi vill ha garanterat plana polygoner kan vi dela in varje fyrhörning i två trianglar, men det är inget Du behöver göra i denna laboration. Radien, r, och antal segment, m, skall enkelt kunna ändras.

Nu till planet som är ortogonalt mot tangenten, t(s). Planet spänns upp av två ortogonala vektorer som tillsammans med tangenten utgör en ortonormal bas för R³. När parametern, s, ändras kan vi tänka oss att detta system åker utmed kurvan. Det finns oändligt många sådana system. Ett alldeles speciellt är det som bildas av tangent, normal och binormal (Frenet koordinatsystemet). Detta system har dock nackdelen att det kan vridas utmed kurvan vilket medför att rektanglarna blir vridna. För att slippa dessa vridna fyrhörningar föreslår jag följande tillvägagångssätt: Då s = s_begin, beräkna den normaliserade (längd ett) tangenten t(s). Detta görs enklast via en differensapproximation; om c(s) är kurvan är ju en tangent c'(s). Bildar vi c'(s) / norm(c'(s)) får vi en normaliserad tangent (norm(vektor) ger den vanliga Euklideska längden av en vektor). Bestäm sedan (slumpmässigt) en normerad vektor, u(s), som är ortogonal mot t(s). Om a och b är två kolonnvektorer och a har längden ett (norm(a) = 1) så är vektorn

ortogonal mot a (d får sedan normaliseras för att få längd ett). Detta är enkelt att inse ty innerprodukten (skalärprodukten) mellan d och a är ju a' *d = a' * b - a' * a * (a' *b) vilken är noll ty a' * a = (längden av a)² = 1. Den tredje riktningen, v(s), kan vi bestämma genom att ortogonalisera en ny slumpvektor mot både t(s) och u(s) (ett annat alternativ är att använda cross). Vektorerna t(s), u(s) samt v(s) utgör nu en ON-bas. Vi tar nu ett steg utmed kurvan och får ett nytt parametervärdet, låt oss kalla det p (s är alltså det föregående parametervärdet och p det nya). Vi bestämmer tangenten, t(p), för detta nya parametervärde. För att slippa få vridna fyrhörningar föreslår jag att man tar u(p) som den ortogonala projektionen av u(s) på planet som är ortogonalt mot t(p). v(p) skall sedan vara ortogonal mot t(p) och u(p). Se till att välja rätt riktning på v(p) så att vi bibehåller orienteringen av koordinatsystemet. Den nya cirkeln skapas sedan i (u(p), v(p))-planet och börjar vi alltid med första segmentpunkten utmed u-axeln slipper vi vridna fyrhörningar.

Följande bild visare en kurva med några utritade (t, u, v)-system. Kurvan är rödprickad. Tangenterna är röda, u-riktningarna är blå och v-riktningarna är gröna. De cirkulära snitten (med indelning) är ritade i svart. De två cyanfärgade linjerna utgör tillsammans med två svarta kordor en rektangel.

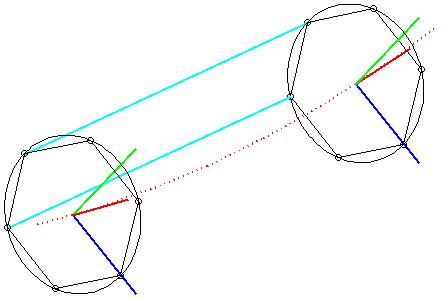
Jag föreslår att Du börjar med att skriva ett program som kan skapa och rita upp (t, u, v)-system samt kurvan så slipper Du nog en hel del avlusningsmöda. Så något i stil med:

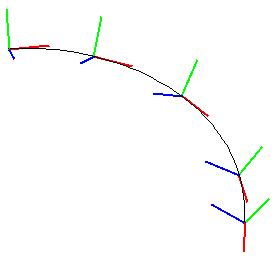
När an väl har gjort indelningen av cirklarna kan man bilda rektanglarna och sedan anropa fill3 för att rita upp dessa.

Nu till den adaptiva steglängdsalgoritmen. Den kan utformas på flera sätt. En osofistikerad metod är följande: Antag att vi har kommit till parametervärdet s_k. Stega sedan med små steg, s > s_k, och beräkna norm(t(s) - t(s_k)). När detta värde överskrider en given tolerans sätter vi s_k+1 till det sista värdet där normen var mindre än toleransen. Vi ser att normen är ett mått på vinkelavvikelsen, v,  mellan tangenterna, ty (om a och b är normerade) gäller att:
 

där v är vinkeln mellan a och b.

Så, om vi begränsar denna norm begränsar vi hur mycket den nya tangenten kan avvika från den gamla. Om vi har en rätlinjig kurva kommer vi att använda ett rörsegement (ty normen blir alltid noll). Träffar vi på en skarp krök ändrar tangenten snabbt riktning varför vi får många korta rörsegment. Rimligtvis borde man blanda in radien, r, i formeln också, men det behöver Du inte göra. Det spelar ju, en inte obetydlig, roll om vi använder smala eller grova rör

Nu till implementationen med surf. Detta kommando kräver inga polygoner utan klarar sig med tre matriser X, Y och Z. (X(j, k), Y(j, k), Z(j, k)) beskriver ytan, och i vårt fall skall punkterna ligga på rörets yta. Man kan då tänka sig att lägga in (x, y, z)-koordinaterna för punkterna i ett plan (ortogonalt mot t(s)) som kolonner i X, Y resp. Z. Anropa surf endast en gång i programmet (man vill inte rita segment för segment utan hela röret på en gång eftersom ljussättningen fungerar bättre då).

Uppgift: implementera ett rör-ritningsprogram enligt ovan. Kurvan skall definieras med en funktion curve(s), som returnerar en kolonnvektor med (x(s), y(s), z(s)). Tangenten skall approximeras med en differensapproximation (inga exakta derivator, med andra ord). Man skall kunna välja att rita med fill3 eller surf. Steglängdsalgoritmen skall vara adaptiv enligt ovan. Man skall kunna variera radie och antalet segment runt röret. Lägg in färg och belysning för att få ett så realistiskt utseende som möjligt!
Testkör åtminstone på följande kurvor. Skriv ut antalet rörsegment som Ditt program använder (jag vill t.ex. för det raka röret endast se ett rörsegment). s antar värdena mellan -1 och 2.

c(s) = (s, 0, 0),   skall ge ett rörsegment

En U-formad (plan) kurva.

c(s) = (-s, 1, 0) då -1 <= s <= 0,
c(s) = (cos(pi (s + 0.5)), sin(pi (s + 0.5)), 0), då 0 <= s <= 1, och
c(s) = (s-1, -1, 0), då 1 <= s <= 2.

Här har jag ritat rören dels med fill3 (det röda) och dels med surf (det gröna). Toleransen i steglängdsalgoritmen är stor (röret blir kantigt). Vi ser tydligt hur adaptiviteten fungerar.

Testa slutligen på spiralen: c(s) = ((3/2) cos(5 s), (s + 2) sin(5 s), s) som med stor tolerans ser ut som

Frivilligt. man kan givetvis bygga ut sitt program med fler effekter. Har man skrivit sitt program på ett strukturerat sätt, är det lätt att lägga in en radie som beror av s. Man kan då rita rör med variabel radie, t.ex. en del av ett svårspelat valthorn.

Genom att anropa sitt rörprogram flera gånger kan man lägga in flera kurvor, t.ex.:

Mer komplicerat är att rita rör vars tvärsnitt inte utgörs av regelbundna polygoner. Vi kanske vill ha ett rör med elliptiskt tvärsnitt till exempel.