Inför tentan
Se länk på kurshemsidan för tid och plats för tentan.

Jag går runt på tentan och svarar på frågor (ordinarie tentatid)
- En gång efter ca en timme
- en gång när det är ca en timme kvar.

Tentan skrivs på papper (med penna) i vanlig tentamenssal.
- Det är viktigt att själv kunna formulera lösningar till problem
- Viktigt att kunna förklara med ord och kod, kommunicera lösningar.

OBS, Inga tillåtna hjäpmedel (förutom penna och suddigummi).
Det finns ett formelblad på kurshemsidan. Formelbladet kommer att biläggas tentan. Bekanta dig med formelbladet före tentan.

Contents

När man löser en tenta:
- Lös de lätta uppgiferna först.
- Svara på frågorna på ett sådant sätt så att jag förstår vad du menar.
- Jag är medveten om att du inte har tillgång till dator när du gör tentan (dvs. jag kommer att ignorera mindre syntaxfel).
- Skriv läsligt
- Skriv inte samma sak flera gånger. Hänvisa med pilar eller markeringar istället (var dock tydlig så att jag förstår vad du menar).
- Svara på frågan.

Tentafrågorna kommer att ligga nära de frågeställningarna som tagits upp på labbarna.

Tentan innehåller någon/några programmeringsuppgifter och några uppgifter numeriska beräkningar. Poängmässigt ungefär hälften av varje. (Lite av programmering ingår i numeriska beräkningar - så ofta blir det lite fler poäng på den delen).
Programmering, lab 1, 2, 3b, 4
Numeriska beräkningar lab 3a, 5, 6, 7

Betygsgränser: 16-23 p. ger betyget 3, 24-31 p. ger betyget 4 och 32 p.
eller mer ger betyget 5. Maxpoäng är 40.

Exempel på en programmeringsuppgift: Uppgift4 2015-04-17

figure(1); clf; hold on;
f = @(x)exp(x).*cos(2*x);
x = linspace(-1,2.5);
plot(x,f(x));

fill([x 2.5 -1],[f(x) -6 -6],'r')
gissn = 0; ratt = 0;
while 1
    sl = rand;                        % slumpa fram ett tal
    [xk,yk,k] = ginput(1);            % läs in ett musklick
    if k~= 1
        break;
    end
    gissn = gissn+1;
    if yk>f(xk)  % klicket var över kurvan
        if sl>0.5  % rätt gissat
            fill([x 2.5 -1],[f(x) 4 4],'g')
            ratt = ratt+1;
        else
            fill([x 2.5 -1],[f(x) 4 4],'r')
        end
    else         % klicket var under kurvan
        if sl<0.5  % rätt gissat
            fill([x 2.5 -1],[f(x) -6 -6],'g')
            ratt = ratt+1;
        else
            fill([x 2.5 -1],[f(x) -6 -6],'r')
        end
    end
    disp([ratt gissn])
end

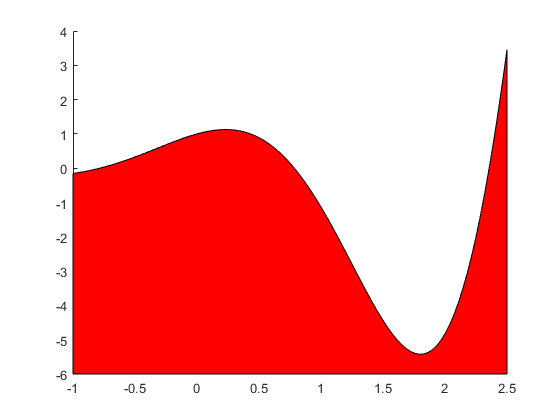
Lite ledning till en programmeringsuppgift på er tenta

Träna på följande uppgift:

Koden nedan ritar ett rutnät med 8x8 rutor: 

figure; hold on;
for i = 1:8
    for j = 1:8
        fill([i i+1 i+1 i],[j j j+1 j+1],'white');
    end
end

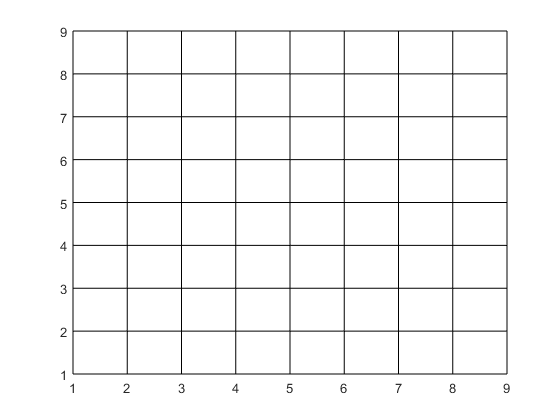
Skriv en sekvens för att markera rutor i rutnätet. Om man klickar i en ruta med vänster musknapp ska rutan färgas röd. Ett klick med höger musknapp ska avbryta loopen. Använd ginput och fill. 

while 1
    [x,y,k] = ginput(1);
    if k ~= 1
        break;
    end
    x = floor(x); y = floor(y);
    fill([x x x+1 x+1],[y y+1 y+1 y],'red');
end

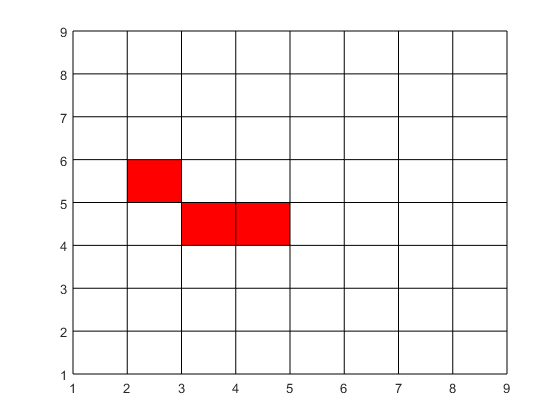
Exempel på frågor om numeriska beräkningar: Uppgift 1 2015-04-17

(a)

figure(1); clf
f = @(x)exp(x).*cos(2*x);
x = linspace(-1,2.5);
plot(x,f(x));
grid on

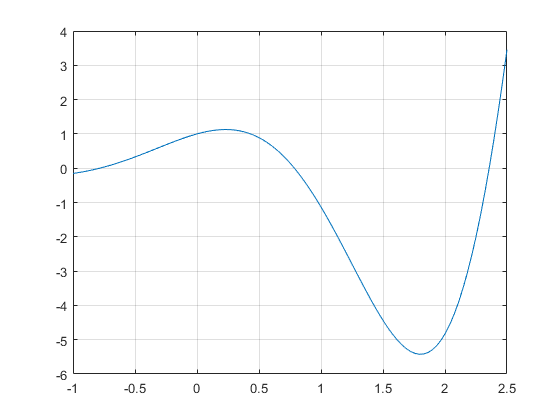
(b) (Obs polylen ingick inte i det årets labbar)

%function L = plgnlgd(x,y)
%  L = 0;
%  for i = 1:length(x)-1
%      L = L + sqrt((x(i+1)-x(i))^2+(y(i+1)-y(i))^2);
%  end

(c)

% steglängd 0.1:
x = linspace(-1,2.5);
lgd = plgnlgd(x,f(x)); % f enligt a) ovan
disp(lgd)

   17.6183

(d)

% bestämmer nollstället mellan 0.5 och 1 med Newtons metod
f = @(x)exp(x)*cos(2*x);
df = @(x)cos(2*x)*exp(x) - 2*sin(2*x)*exp(x);
x = 0.5; tol = 0.5e-4;
for i = 1:10
  h=-f(x)/df(x);
  x=x+h;
  if abs(h)<tol
      break;
  end
end
disp(x)

    0.7854

(e)

% I den sökta punkten är f'(x)=0, dvs. använd Newtons
% metod med f = @(x)cos(2*x)*exp(x) - 2*sin(2*x)*exp(x),
% och df =@(x)- 3*cos(2*x)*exp(x) - 4*sin(2*x)*exp(x).
% sök nollställe nära 1.7

Exempel på en fråga som alltid kommer med Uppgift 2(a) 2015-04-17

% (a) Formulera vänster rektangelregel för beräkning av integraler.

% Jag kommer att be er formulera en av metoderna på tentan,
% denna uppgift kommer att vara värd 3p.
% De metoder som igår i kursen är
%  Newtons metod (lab5)
%  Rektangelreglerna, 4 st (lab6)
%  Eulers metod (lab7)
%
%
% Svara helst i vanligt text på denna fråga. Om man väljer
% att svara i programkod måste man berätta vad de ingående
% storheterna står för. Berätta vad som beräknas, rita tex
% en figur.

% Om du är osäker på hur du ska formulera svaret, skriv gärna
% ner ett förslag och visa mig så ger jag en kommentar på ditt förslag.
% (Jag finns här nästa vecka under labtid i hus Jupiter. Jag rör mig runt
% i huset i huvudsak på plan 3 (samma plan som labsalarna är på).

2 (b)

% Q1 blir vänster rektangelregel, Q2 är höger rektangelregel.
% funktionen f växer på intervallet [a,2.5], så Q2>Q1
% Anmärkning: I anropet
% a = fzero(f,2.7);
% ges ett startvärde utanför figuren till fzero. Frågan är därmed lite felställd
% (eftersom man ju inte får se hur kurvan fortsätter). Ett bättre
% startvärde hade varit 2, dvs anropet
% a = fzero(f,2);
% (Bägge startvärdena konvergerar till samma rot dock)

Uppgift 3 2015-04-17

% (a)
f = @(t,u)-4*u;
[t,U] = ode45(f,[0,0.2],1);

% (b)
% u0 = 1
% u1 = u0 + h*(-4*u0) = 1 + 0.1*(-4*1) = 0.6
% u2 = u1 + h*(-4*u1) = 0.6 + 0.1*(-4*0.6) = 0.36

Uppgift 5 2015-04-17

% (A*A)*v  -> ca 1000^3 + 1000^2 multiplikationer och additioner
% A*(A*v)  -> ca 1000^2 + 1000^2 multiplikationer och additioner


Published with MATLAB® R2017b