Lösningar till intro-tentan i matematik, f.m. 020831 (I1)
- (a)
-
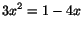
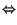
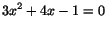
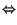
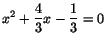
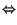
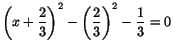
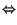
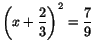
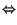
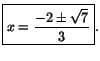
- (b)
- Linjens riktningskoefficient ges av
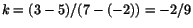 . Enpunktsformeln ger nu att
vilket är samma sak som
. Enpunktsformeln ger nu att
vilket är samma sak som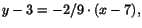
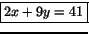 .
.
- (c)
- Betrakta den rätvinkliga triangeln med kateterna
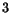 och
och 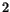 (se Figur
(se Figur ![[*]](http://www.md.chalmers.se/latex_icons//cross_ref_motif.gif) , sista sidan). Låt
, sista sidan). Låt 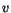 vara vinkeln mellan kateten med sida
vara vinkeln mellan kateten med sida 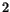 och hypotenusan. Då gäller att
och hypotenusan. Då gäller att
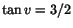 (som önskat), och att
(som önskat), och att 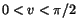 . Hypotenusans längd blir, enligt Pythagoras sats,
. Hypotenusans längd blir, enligt Pythagoras sats,
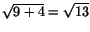 . Det följer att
. Det följer att 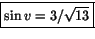 och
och 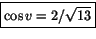 .
.
- (d)
- Vi har
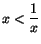
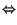
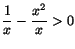
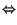
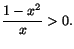
För att olikheten skall gälla skall alltså båda faktorerna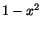 och
och 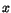 vara positiva eller negativa. De är positiva precis för
vara positiva eller negativa. De är positiva precis för 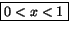 , och negativa för
, och negativa för  . Olikheten gäller alltså för precis dessa
. Olikheten gäller alltså för precis dessa 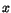 . (Obs! Täljaren
. (Obs! Täljaren 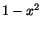 kan faktoriseras som
kan faktoriseras som
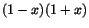 , och en mer allmän lösningsstrategi hade varit att teckenstudera var och en av de tre faktorerna i olikheten i en teckentabell.)
, och en mer allmän lösningsstrategi hade varit att teckenstudera var och en av de tre faktorerna i olikheten i en teckentabell.)
- (a)
-
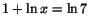
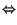
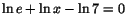
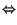
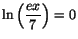
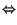
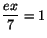
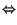
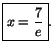
- (b)
-
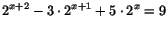
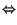
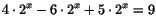
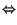
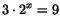
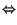
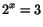
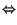
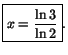
- Vårt ekvationssystem är
Subtrahera ekvation I från ekvation II och subtrahera
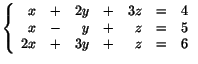
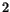 gånger ekvation I från III:
Addera
gånger ekvation I från III:
Addera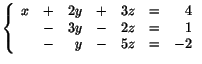
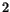 gånger ekvation III till I och addera
gånger ekvation III till I och addera 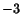 gånger ekvation III till II. Multiplicera därefter ekvation III med
gånger ekvation III till II. Multiplicera därefter ekvation III med 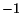 :
Lös systemet:
:
Lös systemet: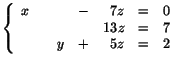 Lösningen blir alltså
Lösningen blir alltså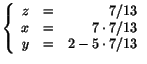
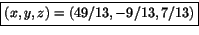 .
.
- Vi visar påståendet med induktion. För
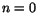 (basfallet) kontrollerar man snabbt att likheten är sann (
(basfallet) kontrollerar man snabbt att likheten är sann (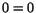 ). Antag att formeln gäller för
). Antag att formeln gäller för 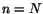 , d.v.s. att
Vi vill nu visa att detta medför att formeln då även gäller för
, d.v.s. att
Vi vill nu visa att detta medför att formeln då även gäller för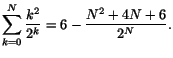
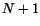 (induktionssteget). Vi har
(induktionssteget). Vi har
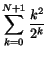
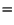
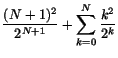
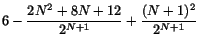
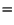
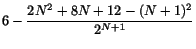
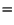
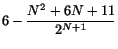
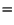
som vi trodde och hoppades! Induktionsaxiomet ger nu att likheten gäller för alla , vilket skulle visas.
, vilket skulle visas.
- Låt
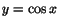 . Då kan vi skriva ekvationen som
Man gissar sig nu fram till rötterna
. Då kan vi skriva ekvationen som
Man gissar sig nu fram till rötterna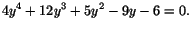
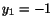 och
och 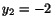 (möjligtvis genom succesiv faktorisering). Faktorsatsen ger att
(möjligtvis genom succesiv faktorisering). Faktorsatsen ger att
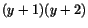 är en faktor i vårt fjärdegradspolynom. Efter division ser man att
är en faktor i vårt fjärdegradspolynom. Efter division ser man att
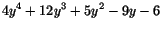
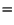
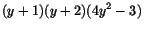
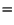
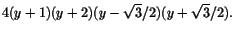
Rötterna till ekvationen ges alltså av
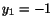 ,
, 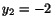 ,
,
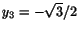 och
och
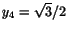 . Vi har nu att lösa ekvationerna
för
. Vi har nu att lösa ekvationerna
för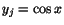
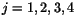 , där
, där 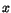 är en vinkel mellan 0 och
är en vinkel mellan 0 och
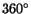 .
För
.
För 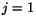 ges lösningen av
ges lösningen av
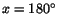 . För
. För 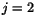 saknas lösning (ty
saknas lösning (ty
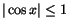 för alla
för alla 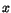 ). För
). För 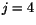 är de godkända lösningarna
är de godkända lösningarna
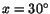 respektive
respektive
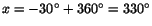 . För
. För 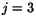 kan vi utnyttja lösningen för
kan vi utnyttja lösningen för 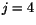 tillsammans med faktumet att
tillsammans med faktumet att 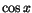 byter tecken om vi adderar (eller subtraherar)
byter tecken om vi adderar (eller subtraherar)
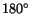 till (från)
till (från) 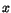 . Lösningarna ges alltså av
. Lösningarna ges alltså av
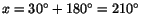 , respektive
, respektive
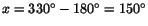 .
.
Alltså, lösningarna ges av
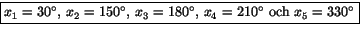 .
.
- (a)
- Kvadratkomplettering:
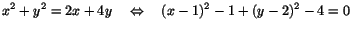 Vi har alltså en cirkel med
Vi har alltså en cirkel med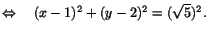
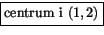 och
och  . På samma sätt för vi
. På samma sätt för vi
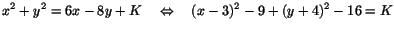 där vi alltså får kräva att
där vi alltså får kräva att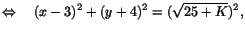
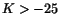 . Den geometriska betydelsen är i detta fallet en cirkel med
. Den geometriska betydelsen är i detta fallet en cirkel med 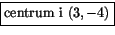 och
och 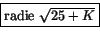 .
.
- (b)
- Låt oss börja med att räkna ut avståndet
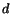 mellan medelpunkterna. Vi har att
mellan medelpunkterna. Vi har att
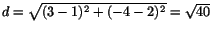 (Pythagoras sats). Cirklarna kan tangera varandra på två sätt. Antingen kan vi ha en yttre tangeringspunkt, d.v.s. cirklarna ligger ``bredvid'' varandra och tangerar, eller en inre tangeringspunkt, d.v.s den ena cirkeln innesluter och tangerar den andra. I det första fallet måste det gälla att summan av cirklarnas radier är lika med avståndet
(Pythagoras sats). Cirklarna kan tangera varandra på två sätt. Antingen kan vi ha en yttre tangeringspunkt, d.v.s. cirklarna ligger ``bredvid'' varandra och tangerar, eller en inre tangeringspunkt, d.v.s den ena cirkeln innesluter och tangerar den andra. I det första fallet måste det gälla att summan av cirklarnas radier är lika med avståndet 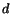 , d.v.s.
, d.v.s.
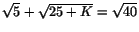 . I det andra fallet måste den ena cirkelns radie vara lika med avståndet
. I det andra fallet måste den ena cirkelns radie vara lika med avståndet 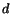 plus den andra cirkelns radie, d.v.s.
plus den andra cirkelns radie, d.v.s.
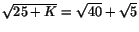 . Vi kan sammanfatta dessa bägge ekvationer som
. Vi kan sammanfatta dessa bägge ekvationer som
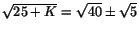 . Vi har nu
. Vi har nu
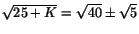
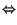
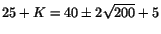
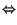
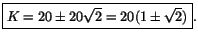
- (a)
- Påståendet är falskt och ett motexempel ges av (t.ex.)
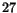 . Det är inte ett primtal. Antag då att det kan skrivas som
. Det är inte ett primtal. Antag då att det kan skrivas som 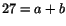 , där
, där 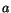 och
och 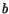 är primtal. Antingen
är primtal. Antingen 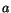 eller
eller 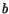 måste då vara jämnt och därmed lika med
måste då vara jämnt och därmed lika med 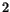 . Men då blir det andra talet lika med
. Men då blir det andra talet lika med 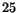 som inte är ett primtal. Vi har en motsägelse.
som inte är ett primtal. Vi har en motsägelse. - (b)
- Påståendet är sant (sambandet mellan aritmetiskt och geometriskt medium). Man har nämligen
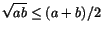
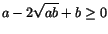
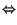
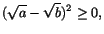
som uppenbarligen är sant.
- Placera tetraedern i ett rätvinkligt koordinatsystem enligt Figur
![[*]](http://www.md.chalmers.se/latex_icons//cross_ref_motif.gif) . Vi får
. Vi får
 . Vi är alltså klara om vi kan visa att detta uttryck är lika med
. Vi är alltså klara om vi kan visa att detta uttryck är lika med 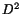 . För att bestämma
. För att bestämma 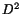 ska vi räkna ut höjden
ska vi räkna ut höjden 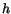 (se Figur
(se Figur ![[*]](http://www.md.chalmers.se/latex_icons//cross_ref_motif.gif) ) i den sneda sidoytan. Basen
) i den sneda sidoytan. Basen 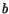 ges av
ges av
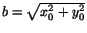 (Pythagoras sats).
(Pythagoras sats).
Betrakta nu den sidoyta (triangel) som ligger i
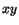 -planet. Om vi kan bestämma höjden
-planet. Om vi kan bestämma höjden 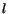 mot hypotenusan i denna triangel så är vi nästan klara. Då gäller ju nämligen att
mot hypotenusan i denna triangel så är vi nästan klara. Då gäller ju nämligen att
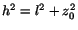 (Pythagoras sats igen). Vi har nu, för att sammanfatta, återfört vårt problem till att bestämma
(Pythagoras sats igen). Vi har nu, för att sammanfatta, återfört vårt problem till att bestämma 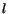 . Men detta är lätt, eftersom vi kan utnyttja likformighet. Vi har1
Det följer att
. Men detta är lätt, eftersom vi kan utnyttja likformighet. Vi har1
Det följer att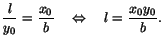
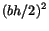
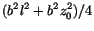
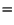
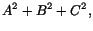
vilket skulle visas.
|
x0
![\includegraphics[width=7cm]{tetraeder.eps}](img131.gif)
|
/ MARTIN BRUNDIN, -02
Jan-Alve Svensson
2002-09-02
![\includegraphics[width=2cm]{triangel.eps}](img127.gif)