Tentamen i TMA 305A Envariabelanalys I, del A,
01 00 02, kl 8.45-11.45.
- 1.
- Bestäm de lokala extrempunkterna till funktionen
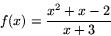
Undersök också funktionen med avseend på konkavitet.
- 2.
- Visa att funktionen
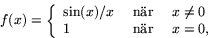
är deriverbar i alla reella tal och bestäm f'(x). Visa också att
f'(x) är kontinuerlig.
- 3.
- Om funktionen f vet man att den är två gånger deriverbar i
alla reella tal och att f''>0. Visa att
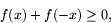
för alla reella tal x.
- 4.
- (a)
- Vad betyder det, enligt definitionen, att
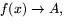 när
när 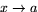 ?
?
- (b)
- Visa, med definitionen, att
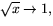 när
när
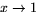 .
.
- (c)
- Visa att om
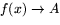 och
och 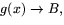 när
när
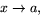 så gäller att
så gäller att 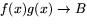 .
.
- 5.
- (a)
- Vad menas med en övre begränsning till en mängd av reella tal?
- (b)
- Formulera och bevisa Inkapslingssatsen.
- (c)
- I satsen används en speciell typ av intervall. Visa med ett
exempel att satsen inte gäller för allmänna intervall.
Jan-Alve Svensson
9/27/2001
![]()
![]()
![]()
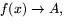 när
när 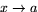 ?
?
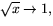 när
när
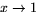 .
.
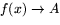 och
och 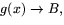 när
när
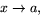 så gäller att
så gäller att 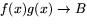 .
.