![]()
Insättning av P4=(1,2,1) ger ![]() så planet går
inte genom P4.
så planet går
inte genom P4.
Svar: Nej.
Detta ger oss att
![]()
Svar: a=-1. Derivatan är kontinuerlig.
Vi söker kritiska punkter: 0=A'(a)=((a+1)-(a+1)2/2)e-a=(1/2)(a+1)(2-a-1)e-a. Detta ger a=-1 eller a=1, där bara a=1 är aktuell (a>0). Vi har A(1)=2e-1.
När ![]() har vi att
har vi att ![]() och när
och när
![]() har vi att
har vi att ![]() . Detta ger att
minsta värde saknas medan det största är 2e-1 eftersom detta är
större än 1/2.
. Detta ger att
minsta värde saknas medan det största är 2e-1 eftersom detta är
större än 1/2.
Svar: Minsta värde saknas, men största värdet är 2e-1.
- (a)
- Låt
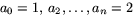 vara en indelning av
intervallet [1,2]. Varje intervall
vara en indelning av
intervallet [1,2]. Varje intervall ![$[a_{i},a_{i+1}],\, 0\leq i\leq
n-1$](img16.gif) innehåller såväl rationella som irrationella punkter, så
funktionens minsta värde där, mi, är 1 medan det största, Mi,
är
innehåller såväl rationella som irrationella punkter, så
funktionens minsta värde där, mi, är 1 medan det största, Mi,
är 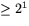 . Detta ger att undersumman är
. Detta ger att undersumman är
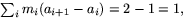 medan översumman är
medan översumman är
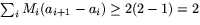 . Varje undersumma är
alltså 1 medan varje översumma är
. Varje undersumma är
alltså 1 medan varje översumma är 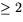 . Detta ger att f inte
är integrerbar på [1,2]
. Detta ger att f inte
är integrerbar på [1,2]