Inför tentamen
Tentamensskrivningen kommer att bestå av 5 uppgifter. Skrivningstiden
är 3 timmar. Varje uppgift kan ge 6 poäng utom en som kan ge 8
poäng.
Poängsumman från examinationen
(tentamen, inlämningsuppgifter, dugga samt bonus från
introduktionskursen) avgör betyget på del A av kursen Envariabelanalys
I. Betygsgränserna är 25 för trea, 32 för fyra och 40 för femma.
Tentamensskrivningen kommer att bestå av tre problem samt två
teoriuppgifter.
Teoriuppgifterna kommer att gälla bevis och definitioner som
genomgåtts under kursen. Vid tentamen ska man känna till och kunna
använda samtliga satser och definitioner.
Följande satser ska dessutom kunna bevisas:
Inkapslingssatsen sidan 84 (överst),
räknereglerna 1 och 2 för
gränsvärden sidan 129,
derivering av en produkt sidan 205,
derivering av en kvot sidan 206,
Kedjeregeln sidan 209,
satsen om
extremvärden sidan 286,
satsen om lokala extremvärden och kritiska
punkter sidan 287,
Medelvärdessatsen sidan 287,
satsen om konstanta
funktioner sidan 288,
satsen om växande/avtagande funktioner sidan 288.
Följande begrepp och definitioner är speciellt viktiga:
funktion, definitionsmängd och värdemängd (sidan 2),
växande/avtagande
funktion (sidan 10),
konkav uppåt/nedåt (sidan 15),
exponentialfunktion,
exponentiellt växande/avtagande (sidorna 17 och 41),
vågrät och lodrät asymptot
(sidan 19),
invers funktion (sidan 32),
den naturliga logaritmen (sidan
40),
arcussinus (sidan 57),
minsta övre och största under begränsning
till en mängd av reella tal (sidan 83),
derivata (sidan 105),
gränsvärde
när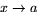 
(sidan 128),
kontinuerlig funktion (sidan 132),
lokal linearisering (sidan 138),
relativt fel (E(x)/(x-a)) (sidan
139),
bestämda integralens definition (sidan 182),
Riemannsumma (sidan
185),
talet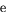 
som gränsvärde (sidan 200),
lokala maxima/minima
och kritisk punkt/värde till en funktion (sidan 241),
inflexionspunkt
(sidan 244),
största/minsta värde (sidan 255),
skalärprodukt av vektorer
(sidan 633),
kryssprodukt av vektorer i rummet (sidan 642).