Tentamen i TMA 305A Envariabelanalys I, del A,
01 00 01, kl 8.45-11.45.
- 1.
- Visa att
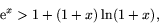
när x>0.
- 2.
- Bestäm den linje som går genom (3,2) och som skär x-
och y-axeln i (x,0) respektive (0,y), så att produkten xy
minimeras.
- 3.
- Låt
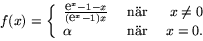
Bestäm 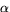 så att f blir kontinuerlig i alla reella tal. Visa
också att f blir deriverbar i x=0, för detta val av
så att f blir kontinuerlig i alla reella tal. Visa
också att f blir deriverbar i x=0, för detta val av 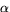 och
bestäm f'(0).
och
bestäm f'(0).
- 4.
- (a)
- Vad betyder det, enligt definitionen, att f(x) är deriverbar
i x=a.
- (b)
- Visa, utgående från definitionen, att f(x)=x2+x-1 är
deriverbar i x=1.
- (c)
- Visa att om funktionerna f(x) och g(x) är deriverbara i x=a, så
är också f(x)g(x) deriverbar i x=a.
- 5.
- Formulera och bevisa medelvärdessatsen. Ge oclså exempel på en tillämpning
av denna sats.
![]()
![]()