Inlämningsuppgift 1 för Envariabelanalys I, del A

 

Tre tunna ogenomskinliga skärmväggar placeras med räta vinklar som i figuren nedan. Skärmarna är 1 m breda och 2 m höga. En ljuskälla placeras längs en cirkelbåge med radie 5 m runt skärmarna, som i figuren till höger nedan.

Man är intresserad av att veta den belysta arean A på den i figuren markerade sidan för olika vinklar $\theta,$ som mäts i radianer.

 

Den vänstra delen av figuren visar skärmväggarnas uppställning. Den högra delen visar konstruktionen sedd uppifrån med ljuskälla och markerad sida.

1. Ange en (obestämd artikel!) formel för funktionen 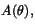$A(\theta),$ där $0<\theta<\pi$.
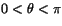2. Skissa grafen till 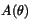$A(\theta)$ med hjälp av en räknedosa.
3. I vilka punkter är 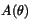$A(\theta)$ kontinuerlig?
4. I vilka punkter är 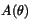$A(\theta)$ deriverbar?

För full poäng krävs att svaren motiveras med kalkyler och argument. Skriv text! Formulera Dig som om Du skrev en förklaring till en kursare, väl insatt i kursen, utan möjlighet till muntlig kommunikation. En eller två A4-sidor bör räcka för lösningen, vid normalstor handskrift.

Handskrivna, lätt läsliga lösningar lämnas i samband med föreläsningen den 25 september. Du får gärna sammarbeta med andra, men Din lösning ska vara personlig. Inga uppskov medges, oavsett vilka skäl som ges!

JAS