Inlämningsuppgift 2
I den här uppgiften ska Du följa en punkts resa längs periferin på ett cyckelhjul. Hjulets nav rör sig framåt med den konstant farten 1 (m/s) i en orealistisk evighet och har den något mindre orealistiska diametern 2 (m). Punkten Du ska följa har markkontakt vid tiden t=0.
![\includegraphics [scale=1]{inl2TMA305aH02figA.eps}](img3.gif) |
![\includegraphics [scale=1]{inl2TMA305aH02figB.eps}](img4.gif) |
Du ska dels beräkna vilken sträcka denna punkt har tillryggalagt vid tiden t, dels vilken medelhastighet den har vid tiden t.
- Ange en parametriserad kurva (x(t),y(t)),
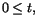 som
beskriver punktens framfart.
som
beskriver punktens framfart.
- I kursen har med visst fog farten för en parametriserad kurva
vid tiden t definierats som
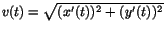 . Beräkna punktens fart vid
tiden t. Antar v(t) ett största och ett minsta värde? I så fall när?
. Beräkna punktens fart vid
tiden t. Antar v(t) ett största och ett minsta värde? I så fall när?
- Beräkna
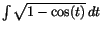 . (Tips: skriv
. (Tips: skriv
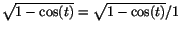 och förläng med
och förläng med
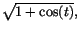 även om detta inte är helt ofarligt. Dela upp Ditt svar i
två fall beroende på tecknet av
även om detta inte är helt ofarligt. Dela upp Ditt svar i
två fall beroende på tecknet av 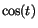 .)
.)
- Funktionen
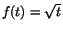 är inte deriverbar i t=0; normalt brukar
man för deriverbarhet i en punkt kräva att funktionen är definierad
i en omgivning till punkten. När a är en ändpunkt
till ett intervall av definitionsmängden kan man tala antingen om höger- eller
vänsterderivatan av funktionen i a, som det eventuella gränsvärdet av
(f(t)-f(a))/(t-a), när
är inte deriverbar i t=0; normalt brukar
man för deriverbarhet i en punkt kräva att funktionen är definierad
i en omgivning till punkten. När a är en ändpunkt
till ett intervall av definitionsmängden kan man tala antingen om höger- eller
vänsterderivatan av funktionen i a, som det eventuella gränsvärdet av
(f(t)-f(a))/(t-a), när
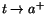 respektive
respektive
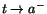 . I fallet med f(t) blir differenskvoten
. I fallet med f(t) blir differenskvoten
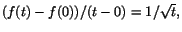 som saknar gränsvärde när
som saknar gränsvärde när
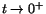 . Så
. Så 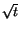 har ingen högerderivata i t=0.
Lite märkligt är det därför att funktionen
har ingen högerderivata i t=0.
Lite märkligt är det därför att funktionen
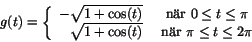
faktiskt är deriverbar i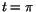 . Visa detta.
. Visa detta.
- Tillryggalagda sträckan s(t) under tiden 0 till t ges av
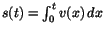 . Beräkna s(t) och skissa dess graf med hjälp av en
räknedosa.
Om Du nu varit så oförsiktig i 3) som jag tror, kommer Du inte att
förstå grafen Du får. Gå tillbaka till 3) och välj konstanter på
olika delar av tallinjen så Din funktion s(t) blir en primitiv
funktion till v(t) på hela icke-negativa tallinjen och så
att s(0)=0.
. Beräkna s(t) och skissa dess graf med hjälp av en
räknedosa.
Om Du nu varit så oförsiktig i 3) som jag tror, kommer Du inte att
förstå grafen Du får. Gå tillbaka till 3) och välj konstanter på
olika delar av tallinjen så Din funktion s(t) blir en primitiv
funktion till v(t) på hela icke-negativa tallinjen och så
att s(0)=0.
- Punktens medelhastighet under tiden från 0 till t ges av
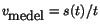 . Skiss grafen till denna funktion med
hjälp av en miniräknare.
. Skiss grafen till denna funktion med
hjälp av en miniräknare.
- (Behöver inte redovisas.) Fixera ett heltal k och bestäm största
och minsta värdet av
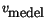 på intervallet
på intervallet
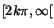 om de finns. Vad händer med
om de finns. Vad händer med
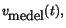 när
när
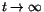 ?
?
För full poäng krävs att Du motiverar Dina ställningstaganden med kalkyler och argument. Dina lösningar ska vara handskrivna och personliga, men samarbete är tillåtet.
Lösningen ska innehålla 1) en parametrisering av punktens bana, en beräkning av 2) v(t), med eventuella största/minsta värde, 3) s(t) och 4) derivatan i delen fyra ovan, samt 5) en skiss av grafen till
Lösningar lämnas i samband med föreläsningen onsdagen den 15 oktober. Inga uppskov medges, oavsett vilka förklaringar som ges. Uppgiften kan ge maximalt tre examinationspoäng.