Kompletterande teori för Envariabelanalys del A på
I
J A S, ht-02
Antag först att vi bara tillåter oss använda naturliga tal. Varje
delmängd till dessa innehåller då ett minsta tal. Men det finns
delmängder till N som inte innehåller något största tal,
t.ex. mängden av jämna naturliga tal.
Om vi däremot tar en delmängd till N som är uppåt begränsad,
dvs varje tal i delmängden är mindre än något fixt naturligt tal K,
så innehåller mängden inte bara ett minsta tal utan också ett
största.
Om vi nu istället tillåter oss (att som vanligt) använda reella
tal. Då har i allmänhet en delmängd till dessa varken ett största
eller ett minsta tal. T.ex. finns det inget största eller minsta tal i
intervallet ]1,2[. Det hjälper inte ens att denna mängd är så väl
uppåt som nedåt begränsad; det finns tal b och B, så att
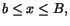 för varje x i mängden.
Däremot finns det gott om så kallade undre begränsningar till
mängden; ett tal b så att för varje x i mängden.
Däremot finns det gott om så kallade undre begränsningar till
mängden; ett tal b så att 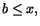 för varje x i
mängden. T.ex. är -1 men också 0 undre begränsningar till
]1,2[. Det finns också gott om övre begränsningar till denna mängd;
ett tal B så att för varje x i
mängden. T.ex. är -1 men också 0 undre begränsningar till
]1,2[. Det finns också gott om övre begränsningar till denna mängd;
ett tal B så att 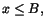 för varje x i mängden. Vi ser att det
finns en största undre begränsning 1, och en minsta övre begränsning
2. Detta är ett allmänt fenomen: för varje x i mängden. Vi ser att det
finns en största undre begränsning 1, och en minsta övre begränsning
2. Detta är ett allmänt fenomen:
Sats 1.1
Varje uppåt begränsad icke-tom mängd av reella tal har en minsta övre begränsning.
För en uppåt begränsad mängd M av reella tal kallas denna minsta
övre begränsning för supremum av mängden och betecknas 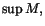 t.ex. har vi
t.ex. har vi ![$\sup ]1,2[=2$](img5.gif) . Beviset av denna sats utnyttjar hur de
reella talen konstrueras och ligger utan för ramen av
envariabelkursen.
På motsvarande vis har en nedåt begränsad icke-tom mängd M av reella tal
en största undre begränsning, som kallas infimum av M och betecknas . Beviset av denna sats utnyttjar hur de
reella talen konstrueras och ligger utan för ramen av
envariabelkursen.
På motsvarande vis har en nedåt begränsad icke-tom mängd M av reella tal
en största undre begränsning, som kallas infimum av M och betecknas
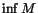 . T.ex. är . T.ex. är ![$\inf ]1,2[=1$](img7.gif) .
I exemplet vi använt är det mycket lätt att bestämma infimum och
supremum. Så är det inte i allmänhet. Om vi t.ex. låter M vara
mänden av tal av formen .
I exemplet vi använt är det mycket lätt att bestämma infimum och
supremum. Så är det inte i allmänhet. Om vi t.ex. låter M vara
mänden av tal av formen 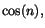 där n är ett heltal, så är det
klart att 1 och -1 är övre respektive undre begränsningar till M
och att M därför har ett infimum och ett supremum. Men det är inte
lätt att förstå vad de är utan att räkna och argumentera.
För att förstå att satsen ovan verkligen innehåller någon information
om de reella talen, kan man tänka sig att man bara tillåter sig att
använda rationella tal. Då gäller inte satsen ovan. Om man t.ex. låter
M vara (den begränsade) mängden av rationella tal x sådana att där n är ett heltal, så är det
klart att 1 och -1 är övre respektive undre begränsningar till M
och att M därför har ett infimum och ett supremum. Men det är inte
lätt att förstå vad de är utan att räkna och argumentera.
För att förstå att satsen ovan verkligen innehåller någon information
om de reella talen, kan man tänka sig att man bara tillåter sig att
använda rationella tal. Då gäller inte satsen ovan. Om man t.ex. låter
M vara (den begränsade) mängden av rationella tal x sådana att
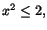 så finns det ingen rationell övre begränsning som är
mindre än varje annan rationell sådan. Om man tillåter sig att använda
de reella talen finns supremum av mängden och är så finns det ingen rationell övre begränsning som är
mindre än varje annan rationell sådan. Om man tillåter sig att använda
de reella talen finns supremum av mängden och är 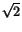 (som inte
är rationellt). (som inte
är rationellt).
Med en avtagande följd av intervall menas en (oändlig) följd
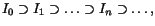 där varje Ik är ett intervall.
I allmänhet finns det då inget reellt tal som ingår i samtliga dessa
intervall. Ett exempel får vi om vi sätter
Ik=]0,1/(k+1)],
där varje Ik är ett intervall.
I allmänhet finns det då inget reellt tal som ingår i samtliga dessa
intervall. Ett exempel får vi om vi sätter
Ik=]0,1/(k+1)],
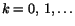 . Om det funnes ett tal r i samtliga dessa intervall
skulle r vara >0, förstås, men samtidigt . Om det funnes ett tal r i samtliga dessa intervall
skulle r vara >0, förstås, men samtidigt 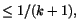 för varje
heltal för varje
heltal 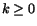 . En orimlighet.
Följande lemma, där man förutsätter att intervallen är slutna (dvs av
formen [a,b]), innehåller därför väsentlig information . En orimlighet.
Följande lemma, där man förutsätter att intervallen är slutna (dvs av
formen [a,b]), innehåller därför väsentlig information
Lemma 1.1 (Inkapslingssatsen)
Om Ik,
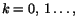 är en avtagande följd av slutna
intervall, så finns det ett reellt tal r som ingår i samtliga intervall.
Bevis. Vi har att
Ik=[ak,bk] för några reella tal
ak och bk. Vi låter M vara mängden av alla sådana
ak. Eftersom följden av intervall är avtagande är varje bk
en övre begränsning till M, som därför har ett supremum r (minsta
övre begränsning). För detta tal r gäller dels att 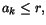 dels
dels 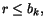 för varje k. Det betyder att r är ett tal som
ingår i samtliga intervall Ik. för varje k. Det betyder att r är ett tal som
ingår i samtliga intervall Ik.
Att
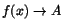 (går mot A) när (går mot A) när
 (går mot a)
ska betyda att värdena till funktionen f ska ligga nära talet A
om x ligger tillräckligt nära a, men (går mot a)
ska betyda att värdena till funktionen f ska ligga nära talet A
om x ligger tillräckligt nära a, men 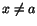 .
Även om denna formulering ganska precist säger vad det hela går ut på
finns det ett problem i den: vad betyder ``nära'' och ``tillräckligt nära''?
Stängt taget är yttrandet `` .
Även om denna formulering ganska precist säger vad det hela går ut på
finns det ett problem i den: vad betyder ``nära'' och ``tillräckligt nära''?
Stängt taget är yttrandet ``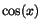 ligger nära ligger nära 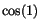 när x
ligger tillräckligt nära 1'' inget påstående eftersom det inte går
att avgöra om det är sant eller falskt. I
matematik använder man definitioner av begrepp för att rigoröst bevisa olika
företelser. Sådana bevis är omöjliga om definitionerna inte är
precisa.
För att precisera vad när x
ligger tillräckligt nära 1'' inget påstående eftersom det inte går
att avgöra om det är sant eller falskt. I
matematik använder man definitioner av begrepp för att rigoröst bevisa olika
företelser. Sådana bevis är omöjliga om definitionerna inte är
precisa.
För att precisera vad
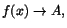 när när
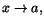 ska
betyda försöker vi först precisera ``närhet''. Ett symmetriskt öppet
intervall runt ett tal r kallas en omgivning till talet. En
omgivning till r har alltså utseendet ska
betyda försöker vi först precisera ``närhet''. Ett symmetriskt öppet
intervall runt ett tal r kallas en omgivning till talet. En
omgivning till r har alltså utseendet
![$]r-\epsilon,r+\epsilon[,$](img26.gif) för
något tal för
något tal 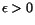 . .
Definition 2.1
Att
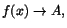 när
 betyder att det till
varje omgivning (varje ``närhet'') till A finns en omgivning (en
``närhet'') till a, så att f( x) ligger i omgivningen till A
när x ligger i omgivningen till a, men 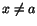 .
Eftersom det ibland är lättare att hantera tal än begrepp som
omgivningar, är det bra att ha följande omformulering av definitionen:
Definition 2.2
Att
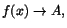 när
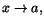 betyder att det till
varje 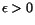 (omgivning till A) finns ett 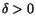
(omgivning till a) så att
Att
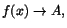 när när
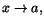 skrivs ofta skrivs ofta
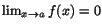 och talet A kallas gränsvärdet av
f(x), när x går mot a. Observera att och talet A kallas gränsvärdet av
f(x), när x går mot a. Observera att
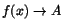 när när
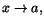 betyder samma sak som betyder samma sak som
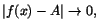 när när
 . .
Exempel 2.1
Visa att
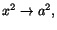 när
 .
Påståendet verkar vara fullkomligt uppenbart på den intuitiva nivån i
vår förståelse av det. Men då bör det heller inte vara särskilt svårt
att visa att det stämmer enligt definitionen.
Antag alltså att vi har ett tal 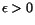 . Vår uppgift är att
tala om hur (eller att) vi kan hitta ett tal . Vår uppgift är att
tala om hur (eller att) vi kan hitta ett tal 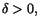 så att så att
Vi har
|x2-a2|=|x-a||x+a|. Om vi förutsätter att 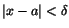 får vi av detta
får vi av detta
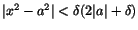 . Allting
kommer alltså att stämma om vi väljer . Allting
kommer alltså att stämma om vi väljer 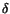 så att så att
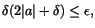 dvs så att dvs så att
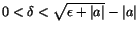 . .
Som vi ser ledde verifikationen av det till synes självklara påståendet
att
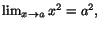 till en del räkningar. Det är
uppenbart att det behövs räkneregler för gränsvärden.
Innan vi går in på det bör det påpekas att det inte är säkert att en
funktion f(x) har något gränsvärde när till en del räkningar. Det är
uppenbart att det behövs räkneregler för gränsvärden.
Innan vi går in på det bör det påpekas att det inte är säkert att en
funktion f(x) har något gränsvärde när
 . I
sådana fall säger man att gränsvärdet inte existerar och symbolen . I
sådana fall säger man att gränsvärdet inte existerar och symbolen
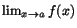 är i så fall meningslös och bör då inte
användas. T.ex saknar är i så fall meningslös och bör då inte
användas. T.ex saknar 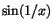 gränsvärde när gränsvärde när
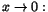 i varje omgivning till 0 finns tal där funktionen antar värdet 1
liksom det finns tal där den antar värdet -1.
En funktion är (uppåt/nedåt) begränsad på en mängd om dess värdemängd där är
(uppåt/nedåt) begränsad. Om
i varje omgivning till 0 finns tal där funktionen antar värdet 1
liksom det finns tal där den antar värdet -1.
En funktion är (uppåt/nedåt) begränsad på en mängd om dess värdemängd där är
(uppåt/nedåt) begränsad. Om
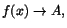 när när
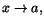 är f(x) begränsad på en omgivning till a: till
är f(x) begränsad på en omgivning till a: till 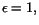 finns
en omgivning till a, så att A-1<f(x)<A+1, när x ligger i
omgivningen till a, men är finns
en omgivning till a, så att A-1<f(x)<A+1, när x ligger i
omgivningen till a, men är 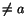 . Man säger att f(x) är
begränsad i närheten av a. Eftersom 1/x inte är begränsad i någon
omgivning till 0, har 1/x inget gränsvärde när . Man säger att f(x) är
begränsad i närheten av a. Eftersom 1/x inte är begränsad i någon
omgivning till 0, har 1/x inget gränsvärde när
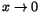 . .
Bevis. 1) Låt 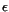 vara givet. Enligt förutsättningarna
finns vara givet. Enligt förutsättningarna
finns 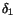 och och 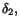 så att så att
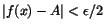 och och
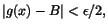 när när
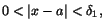 respektive när respektive när
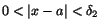 . Detta ger oss . Detta ger oss
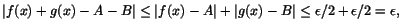 när när
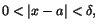 där där 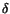 är det minsta av de två talen är det minsta av de två talen
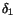 och och 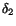 .
2) Låt .
2) Låt 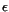 vara givet. Enligt förutsättningarna
finns vara givet. Enligt förutsättningarna
finns 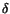 så att så att
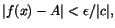 när när
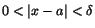 .
Vi har då .
Vi har då
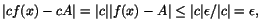 när när
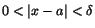 .
3) Vi har, enligt förutsättningarna att .
3) Vi har, enligt förutsättningarna att
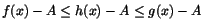 i närheten av a. Givet
i närheten av a. Givet 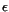 finns vidare finns vidare 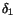 och och
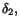 så att så att
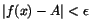 och och
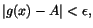 när
när
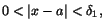 respektive när respektive när
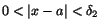 . Från
detta ser vi att . Från
detta ser vi att
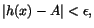 när när
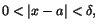 där där
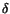 är det minsta av talen är det minsta av talen 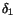 och och 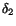 .
4) Vi har .
4) Vi har
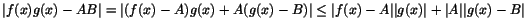 . En konsekvens av förutsättningarna är att
g(x) är uppåt begränsad nära a, låt oss säga av konstanten K. Vi får
då . En konsekvens av förutsättningarna är att
g(x) är uppåt begränsad nära a, låt oss säga av konstanten K. Vi får
då
Enligt 2) går
högra ledet mot
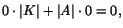
 . Av 3)
följer nu att . Av 3)
följer nu att
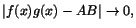 dvs dvs
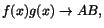 när när
 .
5) Vi har
|1/g(x)-1/B|=|B-g(x)|/(|g(x)||B|) och att |g(x)| är
nedåt begränsad av någon konstant K>0, i en omgivning till a,
eftersom .
5) Vi har
|1/g(x)-1/B|=|B-g(x)|/(|g(x)||B|) och att |g(x)| är
nedåt begränsad av någon konstant K>0, i en omgivning till a,
eftersom
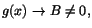 när när
 . Vi får . Vi får
där högra ledet (liksom vänstra) går mot 0, när
 . Påståendet i 5) följer nu från påståendet i 4). . Påståendet i 5) följer nu från påståendet i 4).

Exempel 2.2
Bestäm konstanten a så att gränsvärdet av
existerar när
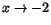 . Bestäm också gränsvärdet för detta a.
Vi skriver på gemensamt bråkstreck och får
Eftersom nämnare går mot 0 när
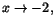 måste vi välja
a, så att även täljaren gör det (annars skulle uttrycket inte vara
begränsat i närheten av -2). Gränsvärdet av täljaren är 4-a+1, så
vi ska välja a=5. Täljaren blir då
x2-4=(x-2)(x+2) och efter
förkortning ska vi bestämma gränsvärdet av (x-2)/(x-1), som enligt
räknereglerna blir -4/-3=4/3, när måste vi välja
a, så att även täljaren gör det (annars skulle uttrycket inte vara
begränsat i närheten av -2). Gränsvärdet av täljaren är 4-a+1, så
vi ska välja a=5. Täljaren blir då
x2-4=(x-2)(x+2) och efter
förkortning ska vi bestämma gränsvärdet av (x-2)/(x-1), som enligt
räknereglerna blir -4/-3=4/3, när
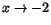 .
I bland har man anledning att använda så kallade ensidiga gränsvärden,
t.ex. vill man kanske bara att x ska närma sig a från höger
(eller uppifrån)(på
tallinjen). .
I bland har man anledning att använda så kallade ensidiga gränsvärden,
t.ex. vill man kanske bara att x ska närma sig a från höger
(eller uppifrån)(på
tallinjen).
Definition 2.3
Att
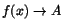 när
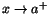 betyder att det
till varje 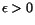 finns ett 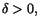 så att
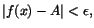 när 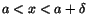 . Man skriver då
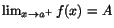 .
På liknande vis definieras gränsvärden då x går mot a nerifrån,
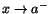 .
I bland, tex när man söker så kallade sneda asymptoter till en
funktion, har man också anledning att undersöka funktioner när .
I bland, tex när man söker så kallade sneda asymptoter till en
funktion, har man också anledning att undersöka funktioner när
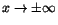 . Definitionen av gränsvärden är i detta fallet: . Definitionen av gränsvärden är i detta fallet:
Definition 2.4
Att
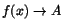 när
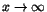 betyder att det
till varje 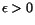 finns ett tal 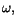 så att
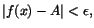 när 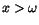 . Man skriver då
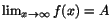 .
På motsvarande sätt definieras gränsvärden när
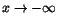 .
Räknereglerna ovan gäller även dessa gränsvärden. .
Räknereglerna ovan gäller även dessa gränsvärden.
Exempel 2.3
Bestäm ett polynom p( x) av så låg grad som möjligt, så att
funktionen
har gränsvärde dels när
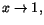 dels när
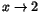 .
Vi har
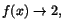 och och
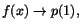 när när
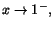 respektive respektive
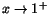 . Vi har också . Vi har också
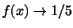 samt samt
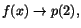 när när
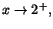 respektive respektive
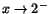 . Vi ska alltså välja p(x),
så att p(1)=2 och p(2)=1/5. Därmed är
p(x)=-9x/5+19/5 . Vi ska alltså välja p(x),
så att p(1)=2 och p(2)=1/5. Därmed är
p(x)=-9x/5+19/5
Exempel 2.4
Bestäm konstanten a så att
f( x)=( x3+3 x2+3)/( x2-4) - ax har ett
gränsvärde när
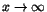 .
Vi skriver på gemensamt bråkstreck och får
f(x)=((1+a)x3+3x2+4ax+3)/(x2-4).
Division med x2 i täljare och nämnare ger nu
Vi ser att vi ska
välja a=-1, för att gränsvärdet ska existera. Det blir då 3/1=3,
när
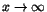 . .
Definition 3.1
En funktion f( x) är kontinuerlig i a om gränsvärdet av f( x) när
 existerar och är f( a).
Exempelvis är funktionen f(x)=x kontinuerlig i varje punkt eftersom
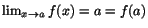 . Mer allmänt ska vi senare se att
de elementära funktionerna är kontinuerliga (eftersom de är
deriverbara, se nedan).
En funktion som är kontinuerlig i varje punkt i sin definitionsmängd
är kontinuerlig (utan specifikation).
Observera att om f(x) är kontinuerlig i a, så är f(x) begränsad
i närheten av a, eftersom f(x) har ett gränsvärde då . Mer allmänt ska vi senare se att
de elementära funktionerna är kontinuerliga (eftersom de är
deriverbara, se nedan).
En funktion som är kontinuerlig i varje punkt i sin definitionsmängd
är kontinuerlig (utan specifikation).
Observera att om f(x) är kontinuerlig i a, så är f(x) begränsad
i närheten av a, eftersom f(x) har ett gränsvärde då
 .
Till exempel finns det ingen möjlighet att bestämma konstanten a,
så att funktionen .
Till exempel finns det ingen möjlighet att bestämma konstanten a,
så att funktionen
blir kontinuerlig. Funktionen saknar gränsvärde när
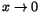 .
Från räknereglerna för gränsvärden följer omedelbart .
Från räknereglerna för gränsvärden följer omedelbart
Sats 3.1
Om f( x) och g( x) är kontinuerliga i x= a, och c är en
konstant, så gäller
- f(x)+g(x) är kontinuerlig i a,
- cf(x) är kontinuerlig i a,
- f(x)g(x) är kontinuerlig i a,
- f(x)/g(x) är kontinuerlig i a, om
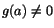 . .
För sammansättningar gäller dessutom
Sats 3.2
Om f(x) är kontinuerlig i g(a) och g(x) är kontinuerlig i a,
så är f(g(x)) kontinuerlig i a.
Bevis. Vi har att
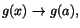 när när
 och att
och att
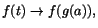 när när
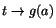 . Satsen
följer nu om vi sätter t=g(x). . Satsen
följer nu om vi sätter t=g(x).
Vi vet t.ex. att f(x)=x är kontinuerlig. Av räkneregelerna följer
nu att x2 är kontinuerlig, liksom xn, där n är ett
heltal. Detta, tillsammans med räknereglerna, ger att alla polynom och
rationella funktioner är kontinuerliga.
Exempel 3.1
Visa att man kan bestämma konstanterna a och b så att funktionen
blir kontinuerlig.
Vi har
x2+3x+2=(x+2)(x+1) och
xkontinuerlig2+x-2=(x+2)(x-1), så
funktionen är definierad utom i 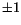 . Kontinuiteten är inget problem
bortanför -2, eftersom funktionen där är summa av två rationella
funktioner.
För att få kontinuitet i -2 ska vi bestämma a, så att det
rationella uttrycket har ett gränsvärde när . Kontinuiteten är inget problem
bortanför -2, eftersom funktionen där är summa av två rationella
funktioner.
För att få kontinuitet i -2 ska vi bestämma a, så att det
rationella uttrycket har ett gränsvärde när
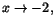 och
sedan välja b som detta gränsvärdet. När och
sedan välja b som detta gränsvärdet. När 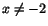 har vi har vi
Eftersom nämnaren
går mot noll när
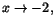 måste även nämnare göra det för att
gränsvärdet ska existera. Detta ger att vi ska välja a så att
(-5)(-1)+a(-3)=0, dvs a=5/3. Talet b ska vara gränsvärdet av måste även nämnare göra det för att
gränsvärdet ska existera. Detta ger att vi ska välja a så att
(-5)(-1)+a(-3)=0, dvs a=5/3. Talet b ska vara gränsvärdet av
som blir
(-2-7/3)/((-3)(-1))=-13/9, når
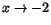 . Svaret är
alltså a=5/3 och b=-13/9. . Svaret är
alltså a=5/3 och b=-13/9.
Man kan ha två lite olika inställningar till begreppet derivata. Det
ena är att derivatan av f(x) i x=a mäter den (momentana) relativa
förändringen av f(x) i x=a. Den andra är att derivatan i x=a
bestämmer (riktningskoefficienten) till tangentlinjen till grafen i
punkten (a,f(a)).
I envariabelanalysen sammanfaller dessa två begrepp, men de skiljer
sig åt i flervariabelanalysen.
Tar vi vår utgångspunkt i den första ikontinuerlignställningen är derivatan av
f(x) i x=a gränsvärdet av differenskvoten
när
 . Funktionen är
deriverbar i a om detta gränsvärde finns. Gränsvärdet betecknas då
f'(a). Om en funktion är deriverbar i varje punkt i sin
definitionsmängd är den deriverbar (utan specifikation). Man använder
då beteckningen f'(x), för derivatan i x och skriver
differenskvoten
(f(x+h)-f(x))/h, och har att f'(x) är gränsvärdet
av detta när . Funktionen är
deriverbar i a om detta gränsvärde finns. Gränsvärdet betecknas då
f'(a). Om en funktion är deriverbar i varje punkt i sin
definitionsmängd är den deriverbar (utan specifikation). Man använder
då beteckningen f'(x), för derivatan i x och skriver
differenskvoten
(f(x+h)-f(x))/h, och har att f'(x) är gränsvärdet
av detta när
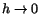 . Flera andra skrivsätt finns t.ex. df/dx=D(f)=f'.
Tar vi i stället vår utgångspunkt i dekontinuerlign andra inställningen ska vi
bestämma talet m, så att linjen y=m(x-a)+f(a) ansluter så väl som
möjligt till grafen av f i punkten (a,f(a)). Avvikelsen
f(x)-m(x-a)+f(a) kallas felet E(x) (när f approximeras med
m(x-a)+f(a)).Vi ska naturligt vis hakontinuerlig att detta fel går mot 0, när . Flera andra skrivsätt finns t.ex. df/dx=D(f)=f'.
Tar vi i stället vår utgångspunkt i dekontinuerlign andra inställningen ska vi
bestämma talet m, så att linjen y=m(x-a)+f(a) ansluter så väl som
möjligt till grafen av f i punkten (a,f(a)). Avvikelsen
f(x)-m(x-a)+f(a) kallas felet E(x) (när f approximeras med
m(x-a)+f(a)).Vi ska naturligt vis hakontinuerlig att detta fel går mot 0, när
 . Men det gör det om f är kontinuerlig i a,
oavsett hur vi väljer m. Om vi däremot kräver att det
relativa felet
R(x)=E(x)/(x-a)=(f(x)-f(a))/(x-a)-m, ska gå mot 0
ser vi att vi måste välja m som (den tidigare) derivatan till f i
x=a.
Derivatan f'(a) bestämmer allstå (riktningskoefficienten för)
tangentlinjen till grafen av f i punkten (a,f(a)). Funktionen
f'(a)(x-a)+f(a) kallas lineariseringen av f i punkten a. När f
är deriverbar i a går alltså inte bara felet, E(x), utan även det relativa
felet, R(x), som görs när f estätt med
f'(a)(x-a)+f(a) mot 0,
när . Men det gör det om f är kontinuerlig i a,
oavsett hur vi väljer m. Om vi däremot kräver att det
relativa felet
R(x)=E(x)/(x-a)=(f(x)-f(a))/(x-a)-m, ska gå mot 0
ser vi att vi måste välja m som (den tidigare) derivatan till f i
x=a.
Derivatan f'(a) bestämmer allstå (riktningskoefficienten för)
tangentlinjen till grafen av f i punkten (a,f(a)). Funktionen
f'(a)(x-a)+f(a) kallas lineariseringen av f i punkten a. När f
är deriverbar i a går alltså inte bara felet, E(x), utan även det relativa
felet, R(x), som görs när f estätt med
f'(a)(x-a)+f(a) mot 0,
när
 .
Låt oss med en gång konstatera att .
Låt oss med en gång konstatera att
Sats 4.1
Om f(x) är deriverbar i a, så är f(x) kontinuerlig i a
Bevis Vi har
f(x)=(x-a)(f(x)-f(a))/(x-a)+f(a), som har
gränsvärdet
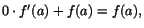 när när
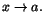  Exemplet f(x)=|x|, är kontinuerlig, men inte
deriverbar i x=0. Differenskvoten där är |x|/x, som antar värdena
Exemplet f(x)=|x|, är kontinuerlig, men inte
deriverbar i x=0. Differenskvoten där är |x|/x, som antar värdena
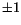 i varje omgivning till 0, och därför saknar gränsvärde när i varje omgivning till 0, och därför saknar gränsvärde när
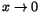 .
För derivator gäller bland annat följande allmänna räkneregler: .
För derivator gäller bland annat följande allmänna räkneregler:
Sats 4.2
Antag att f och g är deriverbara i a och att c är en
konstant. Då gäller
-
(f+g)'(a)=f'(a)+g'(a),
-
(cf)'(a)=cf'(a),
-
(fg)'(a)=f'(a)g(a)+f(a)g'(a),
-
(f/g)'(a)=(f'(a)g(a)-f(a)g'(a))/g(a)2, om
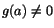 . .
Bevis.
För 1) ska vi betrakta kvoten
(f(x)+g(x)-f(a)-g(a))/(x-a)=(f(x)-f(a))/(x-a)+(g(x)-g(a))/(x-a), som har
gränsvärdet f'(a)+g'(a), när
 .
För 2) ska vi betrakta kvoten
(cf(x)-cf(a))/(x-a)=c(f(x)-f(a))/(x-a), som går mot cf'(a), när .
För 2) ska vi betrakta kvoten
(cf(x)-cf(a))/(x-a)=c(f(x)-f(a))/(x-a), som går mot cf'(a), när
 .
I 3) är kvoten
(f(x)g(x)-f(a)g(a))/(x-a)=((f(x)-f(a))g(x)+f(a)(g(x)-g(a)))/(x-a),
som har gränsvärdet
f'(a)g(a)+f(a)g'(a), när .
I 3) är kvoten
(f(x)g(x)-f(a)g(a))/(x-a)=((f(x)-f(a))g(x)+f(a)(g(x)-g(a)))/(x-a),
som har gränsvärdet
f'(a)g(a)+f(a)g'(a), när
 . Vi
har utnyttjat att g är kontinuerlig i a, eftersom den är
deriverbar där.
I 4) räcker det att kolla fallet när f är konstant 1. Det allmänna
resultatet följer sedan av 3). Kvoten är då . Vi
har utnyttjat att g är kontinuerlig i a, eftersom den är
deriverbar där.
I 4) räcker det att kolla fallet när f är konstant 1. Det allmänna
resultatet följer sedan av 3). Kvoten är då
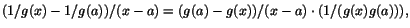 som har
gränsvärdet
-g'(a)/g(a)2, när som har
gränsvärdet
-g'(a)/g(a)2, när
 . Vi har återigen
använt att g är kontinuerlig i a. . Vi har återigen
använt att g är kontinuerlig i a.
Från 3) följer det med induktion att
(xn)'=nxn-1, när 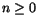 är ett heltal. När n=0 och n=1 kan vi kontroller formeln
direkt: vi ska beräkna gränsvärdet av (1-1)/h=0 respektive
(x+h-x)/h
=1, som naturligtvis är 0 respektive 1 i överensstämmelse med
formeln.
Antag nu att
(xp)'=pxp-1, där är ett heltal. När n=0 och n=1 kan vi kontroller formeln
direkt: vi ska beräkna gränsvärdet av (1-1)/h=0 respektive
(x+h-x)/h
=1, som naturligtvis är 0 respektive 1 i överensstämmelse med
formeln.
Antag nu att
(xp)'=pxp-1, där 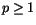 . Vi har då enligt 3)
ovan att . Vi har då enligt 3)
ovan att
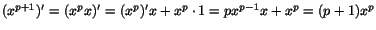 . Formeln följer nu enligt
induktionsprincipen. . Formeln följer nu enligt
induktionsprincipen.
Exempel 4.1
Bestäm, om möjligt, konstanten a så att funktionen
blir deriverbar.
Oavsett hur vi väljer a kommer f'(x)=2x-a, när 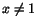 . Så det
enda problemet är derivatan i x=1. Vi har där
(f(x)-f(1))/(x-1)=x(x-a)/(x-1). För att gränsvärdet av detta när . Så det
enda problemet är derivatan i x=1. Vi har där
(f(x)-f(1))/(x-1)=x(x-a)/(x-1). För att gränsvärdet av detta när
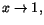 ska existera måste vi ha a=1 och vi får då
f'(1)=1. ska existera måste vi ha a=1 och vi får då
f'(1)=1.
För att bestämma derivatan av en exponentialfunktion ax ska vi
undersöka
(1/h)(ax+h-ax)=(1/h)(ah-1)ax, när
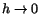 . Vi ser att om vi
kan välja a så att . Vi ser att om vi
kan välja a så att
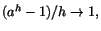 när när
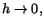 så får vi
D(ax)=ax. Detta tyder på att vi då ska ha
så får vi
D(ax)=ax. Detta tyder på att vi då ska ha
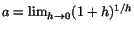 . Man kan visa att detta verkligen
fungerar och vi kan välja . Man kan visa att detta verkligen
fungerar och vi kan välja
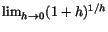 som en
definition av talet e. Vi har alltså som en
definition av talet e. Vi har alltså
D(ex)=ex.
Allmänt har
vi att
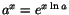 och differenskvoten blir och differenskvoten blir
när
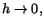 så så
Genom att studera grafen till en inverterbar funktion f och
grafen till dess invers f-1 kan man visa
Sats 5.1
Antag att f är inverterbar och deriverbar i a med derivata 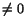 . Då är f-1 deriverbar i f( a) med derivata
( f-1)'( f( a))=1/ f'( a).
Vi kan också formulera det så att
(f-1)'(x)=1/f'(f-1(x)).
Med detta kan vi bestämma derivatan till 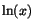 som är inversen till
ex. Eftersom
D(ex)=ex ger satsen att som är inversen till
ex. Eftersom
D(ex)=ex ger satsen att
För att derivera xp, där p är en konstant gör vi omskrivningen
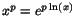 och ser den som en sammansatt funktion; en
logaritmfunktion följd av en exponentialfunktion. För att derivera
sammansättningar har man användning av följande och ser den som en sammansatt funktion; en
logaritmfunktion följd av en exponentialfunktion. För att derivera
sammansättningar har man användning av följande
Sats 5.2 (Kedjeregeln)
Antag att f(x) är deriverbar i g(a) och att g(x) är deriverbar
i a. Då är f(g(x)) deriverbar i a med derivata f'(g(a))g'(a).
Detta kan också skrivas
(f(g(x)))'=f(g(x))g'(x). I detta sammanhan
kallas g'(x) för den sammansatta funktionens inre derivata.
Bevis. Vi ska undersöka kvoten
(f(g(x))-f(g(a)))/(x-a). Eftersom f är deriverbar i g(a) har vi
att
f(g(x))-f(g(a))=f'(g(a))(g(x)-g(a))+R(g(x))(g(x)-g(a)), där R(x) är
det relativa felet till den linjära approximationen av f(x) i
g(a). Minns att
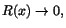 när när
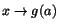 .
Eftersom g(x) är deriverbar i a är den kontinuerlig i a, så .
Eftersom g(x) är deriverbar i a är den kontinuerlig i a, så
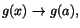 när när
 . Detta ger att . Detta ger att
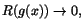 när när
 .
För den ursprungliga kvoten får vi nu .
För den ursprungliga kvoten får vi nu
där högra ledet går mot
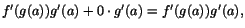 när
när
 . .
Med satsen får vi att derivatan av
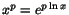 är är
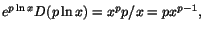 eller eller
D(xp)=pxp-1.
För att härleda derivator till trigonometriska funktioner behöver vi
ett så kallat standard gränsvärde (eller ``känt'' gränsvärde). Det
gäller att
Från en figur ser man att
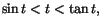 när när 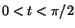 . Från
detta får vi . Från
detta får vi 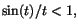 men också men också
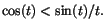 Genom att
byta t mot -t ser vi att dessa olikheter även gäller när Genom att
byta t mot -t ser vi att dessa olikheter även gäller när
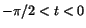 . Från en figur ser man också att . Från en figur ser man också att
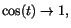 när
när
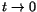 . Vi får nu att även . Vi får nu att även
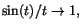 när när
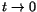 .
För att derivera .
För att derivera 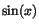 ska vi undersöka kvoten ska vi undersöka kvoten
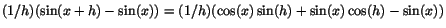 Vi ser att vi behöver undersöka
Vi ser att vi behöver undersöka
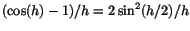 där
vi använt att där
vi använt att
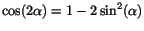 . Standard
gränsvärdet ovan ger alltså att . Standard
gränsvärdet ovan ger alltså att
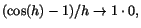 när när
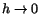 . Vår differenskvot för derivatan av . Vår differenskvot för derivatan av 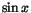 har
därför gränsvärdet har
därför gränsvärdet
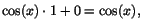 när när
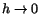 .
V har alltså .
V har alltså
För att derivera 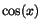 räcker det nu att göra omskrivningen räcker det nu att göra omskrivningen
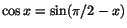 . Kedjeregeln ger nu . Kedjeregeln ger nu
För att derivera 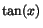 kan vi skriva kan vi skriva
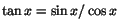 och
derivera som en kvot. Vi får då och
derivera som en kvot. Vi får då
Båda är
användbara uttryck för derivatan av tangensfunktionen.
Arcusfunktionerna är inverser till de trigonometriska funktionerna med
lämpligt inskränkta definitionsmängder och de är därför
deriverbara. För att härleda deras derivator kan man använda
kedjeregeln och t.ex. identiteten
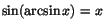 . Derivering
av detta ger . Derivering
av detta ger
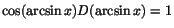 . Eftersom . Eftersom
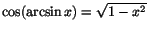 får vi får vi
På samma vis ger derivering av
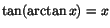 att att
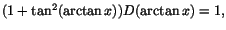 så så
Ett viktigt uppgift, som ofta dyker upp i praktiken, är att försöka
bestämma det största som en funktion antar. (Så kallade
optimeringsproblem.)
Från början kan vi konstatera att det inte alltså är säkert att en
funktion antar ett största och ett minsta värde. T.ex antar
funktionen f(x)=x, varken ett största eller ett minsta värde på
intervallet ]1,2[. Funktionen antar ett minsta värde på intervallet
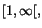 men inget största värde. Funktionen men inget största värde. Funktionen
antar varken ett största eller minsta värde på intervallet [-1,1].
Därför innehäller följande sats väsentlig information
Sats 6.1
Om f(x) är kontinuerlig på det slutna begränsade intervallet
[a,b], så antar funktionen ett största och ett minsta värde i intervallet.
För att visa satsen ska vi först visa
Lemma 6.1
Om f(x) är kontinuerlig på det slutna begränsade intervallet
[a,b], så är f(x) uppåt begränsad på intervallet.
Bevis. Antag att påståendet inte stämmer. Om vi delar
intervallet mitt itu kommer f då att inte vara uppåt begränsad på minst en av
de två delarna. Beteckna denna del [a1,b1]. Dess längd är
(b-a)/2. Proceduren kan
upprepas och vi får en hälft [a2,b2] av [a1,b1] där
funktionen inte är uppåt begränsad. Upprepning leder till en av tagande
följd av intervall [an,bn] av längd (b-a)/2n, där f inte är
uppåt begränsad. Inkapslings satsen ger att det finns ett tal r som ingår
i samtliga intervall. Eftersom f är kontinuerlig i r gäller att
f är begränsad i en omgivning till r. Men en omgivning till r
innehåller något [an,bn] där f inte är uppåt begränsad. En
orimlighet. Antagandet att f inte är uppåt begränsad är alltså fel
och därmed är f uppåt begränsad på intervallet.
Bevis av satsen Vi vet att f är uppåt begränsad. Det
betyder att värdemängden till f har en minsta övre begränsning M,
så 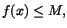 för alla x i [a,b] och M är det minsta talet
med denna egenskap. Antag nu att f(x) inte antar värdet
M. Funktionen 1/(M-f(x)) är då kontinuerlig och positiv på
[a,b]. Den är därför uppåt begränsad av någon konstant, säg m>0. Vi
har då för alla x i [a,b] och M är det minsta talet
med denna egenskap. Antag nu att f(x) inte antar värdet
M. Funktionen 1/(M-f(x)) är då kontinuerlig och positiv på
[a,b]. Den är därför uppåt begränsad av någon konstant, säg m>0. Vi
har då
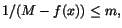 eller eller
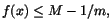 vilket strider mot
att M var den minsta övre begränsningen till f. Alltså måste f
anta värdet M på intervallet [a,b].
Funktionen -f är också kontinuerlig på [a,b] och antar, enligt vad
vi visat, ett största värde, låt oss kalla det L, där. -L är då
det minsta värde som f antar på intervallet. vilket strider mot
att M var den minsta övre begränsningen till f. Alltså måste f
anta värdet M på intervallet [a,b].
Funktionen -f är också kontinuerlig på [a,b] och antar, enligt vad
vi visat, ett största värde, låt oss kalla det L, där. -L är då
det minsta värde som f antar på intervallet.
Definition 6.1
En funktion f har ett lokalt maximum/minimum i en punkt a om
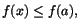 respektive 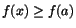 , för alla x i en
omgivning till a.
Sats 6.2
Antag att f är deriverbar i a och har ett lokalt maximum eller
minimum i denna punkt. Då är f'(a)=0.
Bevis. Antag att f har ett lokalt maximum i
a. Differenskvoten är
Q=(f(x)-f(a))/(x-a). När x>a är detta
uttryck 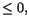 och när x<a är det och när x<a är det 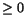 . Av detta följer att
gränsvärdet f'(a) av Q måste vara noll, när . Av detta följer att
gränsvärdet f'(a) av Q måste vara noll, när
 .
Beviset när f har ett loklat minimum i a är
liknande. .
Beviset när f har ett loklat minimum i a är
liknande.
Observera att f'(a)=0 inte i allmänhet betyder att f har ett
lokalt maximum eller minimum i a. T.ex. har f(x)=x3,
derivatan f'(0)=0, men f har varken lokalt maximum eller minimum i
0. Talet 0 är det man brukar kalla en terrasspunkt till funktionen.
Följande sats, som knyter ihop kontinuitet och deriverbarhet, brukar
kallas Rolles sats
Sats 6.3
Antag att f är kontinuerlig på [a,b] och deriverbar på
]a,b[. Om då f(a)=f(b), så finns det ett tal c, så att
a<c<b, och f'(c)=0.
Bevis. Om f är konstant så är f'(c)=0, för varje val av
c mellan a och b. Annars antar f antingen ett största eller
ett minsta värde (f är kontinuerlig på [a,b]) i någon punkt c
mellan a och b. Eftersom f är deriverbar i c är
f'(c)=0.
Den förmodligen allra viktigaste satsen om deriverbara funktioner är
Sats 6.4 (Medelvärdessatsen)
Antag att f är kontinuerlig på [ a, b] och deriverbar i ] a, b[. Då
finns ett tal c mellan a och b, så att
Bevis. Sätt
h(x)=f(x)-(f(b)-f(a))(x-a)/(b-a)-f(a). Då är
h kontinuerlig på [a,b] och deriverbar på (a,b). Dessutom är
h(a)=0=h(b), så Rolles sats ger ett c mellan a och b, så att
0=h'(c)=f'(c)-(f(b)-f(a))/(b-a). En rad andra kända påståenden om deriverbara funktioner är
konsekvenser av medelvärdessatsen.
En rad andra kända påståenden om deriverbara funktioner är
konsekvenser av medelvärdessatsen.
Sats 6.5
Antag att f är kontinuerlig på [ a, b] och deriverbar i ] a, b[.
- Om f'(x)>0, på ]a,b[, så är f strängt växande på [a,b],
- om
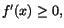 på ]a,b[, så är så är f växande på [a,b]. på ]a,b[, så är så är f växande på [a,b].
Bevis. Antag att x0<x1 är två tal i
[a,b]. Medelvärdessatsen ger ett c mellan x0 och x1, så
att
f(x1)-f(x0)=f'(c)(x1-x0). I fall 1) ger detta
f(x1)>f(x0), och i fall 2)
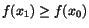 . .
Det är klart att om f är konstant så är f'(x)=0, för alla x. Men
omvändningen gäller också:
Sats 6.6
Om f är kontinuerlig på [a,b] och deriverbar i ]a,b[, och
f'(x)=0 för alla x mellan a och b, så är f konstant på [a,b].
Bevis. Tag två tal x0 och x1 i
[a,b]. Medelvärdessatsen ger ett c mellan dessa båda tal, så att
f(x1)-f(x0)=f'(c)(x1-x0)=0. Detta betyder att f är
konstant på [a,b].
Ofta, t.ex. i derivatans definition, dyker det upp så kallade
gränsvärden av typen ``0/0''. l'Hospitals regel ger hjälp vid
beräkning av sådana gränsvärden.
Antag till exempel att vi vill beräkna gränsvärdet av f(x)/g(x), när
 och
att f(x) och g(x) båda år deriverabara i x=a har
f(a)=g(a)=0. Kvoten kan då skrivas och
att f(x) och g(x) båda år deriverabara i x=a har
f(a)=g(a)=0. Kvoten kan då skrivas
som går mot f'(a)/g'(a), om 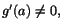 när när
 . Vad
händer om g'(a)=f'(a)=0 i detta uttryck?. För att svara på frågan
behöver vi en generalisering av medelvärdessvärdessatsen. . Vad
händer om g'(a)=f'(a)=0 i detta uttryck?. För att svara på frågan
behöver vi en generalisering av medelvärdessvärdessatsen.
Sats 7.1
Antag att f och g är kontinuerliga på [ a, b] och deriverbara i
] a, b[. Om
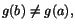 så finns ett tal c mellan a och
b, så att
Vi får den tidigare medelvärdessatsen om vi ovan sätter g(x)=x.
Bevis. Sätt
h(x)=f(x)-(f(b)-f(a))(g(x)-g(a))/(g(b)-g(a))-f(a). Vi har då att
h(a)=0=h(b) och förutsättningarna i Rolles sats är uppfyllda. Detta
ger ett c mellan a och b, så att
0=h'(c)=f'(c)-(f(b)-f(a))g'(c)/(g(b)-g(a)).
Sats 7.2 (l'Hospitals regel)
Antag att f och g är deriverbara i
en omgivning till a och f( a)=0= g( a), samt att
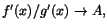 när
 .
Då gäller även att
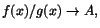 när
 . 
Bevis. Enligt utvidgningen av medelvärdessatsen finns det ett
tal c mellan x och a, så att
f(x)/g(x)=f'(c)/g'(c). Vi ser att
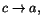 när när
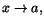 vilket ger
resultatet. vilket ger
resultatet.
Konklusionen i satsen kan också skrivas
om f(a)=g(a)=0, och gränsvärdet i höger led existerar.
Förutsättningen att gränsvärdet är av typen ``0/0'' är väsentlig!
T.ex. har kvoten (x-1)/x gränsvärdet 0, när
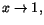 medan
D(x-1)/D(x)=1/1, har gränsvärdet 1.
medan
D(x-1)/D(x)=1/1, har gränsvärdet 1.
Exempel 7.1
Beräkna gränsvärdet av
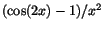 när
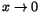 .
Vi ser att det är fråga om ett gränsvärde av typen ``0/0''. Uttrycket
har därför samma gränsvärde som kvoten
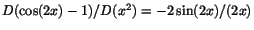 . Även här är det fråga om ett
gränsvärde av typen ``0/0''. Kvoten har därför samma gränsvärde som . Även här är det fråga om ett
gränsvärde av typen ``0/0''. Kvoten har därför samma gränsvärde som
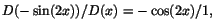 som går mot -1, när som går mot -1, när
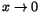 . .
Exempel 7.2
Undersök om man kan bestämma konstanten a, så att funktionen
blir deriverbar. Är derivatan kontinuerlig?
Det är inget problem att derivera med hjälp av formler bortanför
x=0. För att undersöka derivatan i x=0, ska vi undersöka
differenskvoten
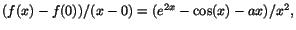 när när
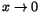 . Vi ser att det är fråga om ett gränsvärde av typen
``0/0,'' oavsett vad a är. Kvoten har därför samma gränsvärde som . Vi ser att det är fråga om ett gränsvärde av typen
``0/0,'' oavsett vad a är. Kvoten har därför samma gränsvärde som
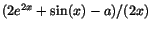 . Här ser vi att nämnaren går mot 0, när . Här ser vi att nämnaren går mot 0, när
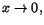 så även täljaren måste göra det för att gränsvärdet
ska existera. Detta ger a=2. Kvoten ger då ett gränsvärde av typen
``0/0,'' och har därför samma gränsvärde som så även täljaren måste göra det för att gränsvärdet
ska existera. Detta ger a=2. Kvoten ger då ett gränsvärde av typen
``0/0,'' och har därför samma gränsvärde som
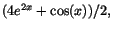 dvs 5/2, när
dvs 5/2, när
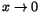 . Vi har alltså att f är deriverbar
även i x=0, om vi sätter a=2, och derivatan där är då f'(0)=5/2.
Vi har följande formel för derivatan: . Vi har alltså att f är deriverbar
även i x=0, om vi sätter a=2, och derivatan där är då f'(0)=5/2.
Vi har följande formel för derivatan:
Av formeln ser vi att f'(x) är kontinuerlig utom möjligen i x=0.
För att undersöka kontinuitet där ska vi undersöka gränsvärdet av
kvoten
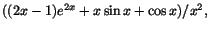 när när
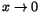 .
För kontinuitet i x=0 krävs att detta existerar och är f'(0)=5/2.
Vi ser att det är fråga om ett gränsvärde av typen ``0/0'' och kvoten
har därför samma gränsvärde som .
För kontinuitet i x=0 krävs att detta existerar och är f'(0)=5/2.
Vi ser att det är fråga om ett gränsvärde av typen ``0/0'' och kvoten
har därför samma gränsvärde som
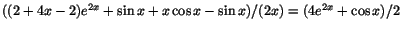 . Denna sista kvot har gränsvärdet
(4+1)/2=5/2=f'(0), när . Denna sista kvot har gränsvärdet
(4+1)/2=5/2=f'(0), när
 . Detta visar att f'(x) är
kontinuerlig. . Detta visar att f'(x) är
kontinuerlig.
Antag att f(x) är en begränsad funktion på (det begränsade)
intervallet [a,b]. Till en sådan funktion kan man bilda så kallade
över- och undersummor.
Dela in intervallet i delintervall genom att välja ett antal (n+1)
punkter i det:
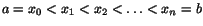 . Välj tal Mk
och
mk, så att . Välj tal Mk
och
mk, så att
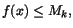 respektive respektive
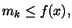 när när
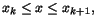
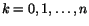 .
Talen .
Talen
och
kallas då över- respektive undersumma till f(x) över intervallet
[a,b].
Varje översumma S är större än varje undersumma s, även om de
kommer från olika indelningar av intervallet [a,b].
Enligt fullständighetsegenskapen hos de reella talen finns det ett
största tal U mindre än eller lika med alla översummor till f(x)
över [a,b]. På motsvarande vis finns det ett minsta tal L större
än alla undersummor och vi har 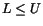 . Om det inträffar att de två
talen L och U är lika är f(x) integrerbar över [a,b]: . Om det inträffar att de två
talen L och U är lika är f(x) integrerbar över [a,b]:
Definition 8.1
En begränsad funktion f( x) på [ a, b] är
integrerbar över
intervallet om det finns precis ett tal mindre än eller lika med
alla översummor och större än eller lika med alla undersummor till
f( x) över [ a, b]. Detta tal betecknas då
Ett exempel på en funktion som inte är integrerbar över [0,1] får
man om man sätter f(x)=1, när x är kvot mellan två heltal och
f(x)=0, annars. Det finns (i detta fall rent av) en minsta
översumma som är U=1 och en största undersumma som är L=0.
Vi behöver veta att välkända funktioner är integrerbara:
Sats 8.1
Antag att f(x) är kontinuerlig på [a,b]. Då är f(x)
integrerbar över [a,b].
Anm. Minns att en kontinuerlig funktion på ett slutet
begränsat intervall antar så väl ett största som ett minsta värde. Vi
kallar skillnaden mellan dessa för variationen av f(x) på
intervallet.
Bevis. Vi kan bevisa påståendet genom att för varje tal
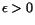 bestämma en översumma S och en undersumma s, så att bestämma en översumma S och en undersumma s, så att
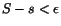 .
För att klara detta räcker det att visa att vi kan dela upp [a,b] i
delar så att f(x) har variation .
För att klara detta räcker det att visa att vi kan dela upp [a,b] i
delar så att f(x) har variation
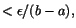 på varje del.
Antag att detta inte är möjligt. Dela
[a,b]=[a0,b0] mitt
itu. Då är det heller inte möjligt på minst en av de två delarna, låt
oss säga [a1,b1]. Proceduren kan upprepas och vi får en
avtagande följd av intervall
In=[an,bn], på varje del.
Antag att detta inte är möjligt. Dela
[a,b]=[a0,b0] mitt
itu. Då är det heller inte möjligt på minst en av de två delarna, låt
oss säga [a1,b1]. Proceduren kan upprepas och vi får en
avtagande följd av intervall
In=[an,bn],
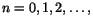 av längd (b-a)/2n, sådana att f(x) har variation
av längd (b-a)/2n, sådana att f(x) har variation
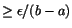 på varje In.
Enligt inkapslingssatsen finns ett tal r som ingår i samtliga dessa
intervall. Eftersom f(x) är kontinuerlig i r finns en omgivning
till r där f(x) har en variation på varje In.
Enligt inkapslingssatsen finns ett tal r som ingår i samtliga dessa
intervall. Eftersom f(x) är kontinuerlig i r finns en omgivning
till r där f(x) har en variation
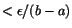 . Men denna
omgivning innehåller också In, när n är tillräckligt stort. En
motsägelse. Detta visar i sin tur satsen. . Men denna
omgivning innehåller också In, när n är tillräckligt stort. En
motsägelse. Detta visar i sin tur satsen.

Vi ska se att man kan integrera kontinuerliga funktioner genom att
``derivera baklänges,'' men behöver för detta
Sats 9.1 (Integralkalkylens medelvärdessats)
Antag att f( x) är
kontinuerlig på [ a, b]. Då finns ett tal 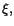
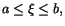 så att
Beviset bygger på den så kallade satsen om mellanliggande värden: Om
f(x) är kontinuerlig på ett intervall och antar värdena A och B
där, så antar f(x) även alla värden mellan dessa båda tal på intervallet.
Bevis. Eftersom f(x) är kontinuerlig på [a,b], antar den
ett största värde M och ett minsta värde m på intervallet. Detta
ger oss översumman M(b-a) samt undersumman m(b-a) och
Enligt satsen om mellanliggande värden finns nu ett tal 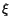 mellan
a och b, så att mellan
a och b, så att
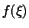 är mittersta ledet. är mittersta ledet.

Sats 9.2
Antag att f( x) är kontinuerlig på [ a, b]. Då är
kontinuerlig på [ a, b] och deriverbar på ] a, b[ med
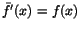 .
Bevis. Vi ska undersöka differenskvoten
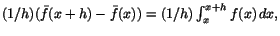 när när
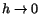 . Enigt integralkalkylens medelvärdes sats är detta . Enigt integralkalkylens medelvärdes sats är detta
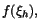 för något för något 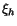 mellan x och x+h. Vi ser att mellan x och x+h. Vi ser att
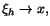 när när
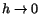 . Eftersom f(x) är
kontinuerlig ger detta att . Eftersom f(x) är
kontinuerlig ger detta att
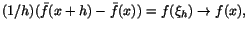 när när
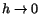 .
Att .
Att 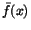 dessutom är kontinuerlig när x=a och x=b följer
direkt av integralkalkylens medelvärdessats. T.ex är dessutom är kontinuerlig när x=a och x=b följer
direkt av integralkalkylens medelvärdessats. T.ex är
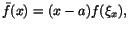 för något för något 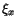 mellan x och
a. Låter vi mellan x och
a. Låter vi
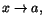 ger detta ger detta
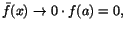 som ju är
som ju är 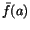 . På samma sätt är . På samma sätt är
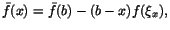 för något tal för något tal 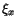 mellan x och b, vilket ger att
mellan x och b, vilket ger att
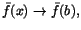 när
när
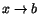 . .

Sats 9.3 (Integralkalkylens huvudsats)
Antag att f( x) är
kontinuerlig på [ a, b] och att F( x) är en deriverbar funktion
sådan att F'( x)= f( x), för alla x i intervallet. Då gäller
Anm. Det är brukligt att skriva
![$\Big[F(x)\Big]_{a}^{b}$](img41A.gif) för
talet F(b)-F(a). En funktion F(x) som i satsens förutsättning är
en primitiv funktion till f(x). Enligt tidigare satsen är för
talet F(b)-F(a). En funktion F(x) som i satsens förutsättning är
en primitiv funktion till f(x). Enligt tidigare satsen är
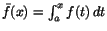 en primitiv funktion till f(x). en primitiv funktion till f(x).
Bevis. Sätter vi
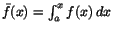 har vi har vi
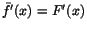 där båda funktionerna är deriverbara på (minst)
]a,b[ och kontinuerliga på [a,b]. Detta ger att där båda funktionerna är deriverbara på (minst)
]a,b[ och kontinuerliga på [a,b]. Detta ger att
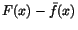 är en konstant, låt oss säga C, på intervallet. Av detta ser vi att
är en konstant, låt oss säga C, på intervallet. Av detta ser vi att
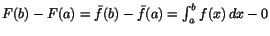 . .
Jan-Alve Svensson
2002-09-23
|
![]() där varje Ik är ett intervall.
I allmänhet finns det då inget reellt tal som ingår i samtliga dessa
intervall. Ett exempel får vi om vi sätter
Ik=]0,1/(k+1)],
där varje Ik är ett intervall.
I allmänhet finns det då inget reellt tal som ingår i samtliga dessa
intervall. Ett exempel får vi om vi sätter
Ik=]0,1/(k+1)],
![]() . Om det funnes ett tal r i samtliga dessa intervall
skulle r vara >0, förstås, men samtidigt
. Om det funnes ett tal r i samtliga dessa intervall
skulle r vara >0, förstås, men samtidigt ![]() för varje
heltal
för varje
heltal ![]() . En orimlighet.
Följande lemma, där man förutsätter att intervallen är slutna (dvs av
formen [a,b]), innehåller därför väsentlig information
. En orimlighet.
Följande lemma, där man förutsätter att intervallen är slutna (dvs av
formen [a,b]), innehåller därför väsentlig information
![]() till en del räkningar. Det är
uppenbart att det behövs räkneregler för gränsvärden.
Innan vi går in på det bör det påpekas att det inte är säkert att en
funktion f(x) har något gränsvärde när
till en del räkningar. Det är
uppenbart att det behövs räkneregler för gränsvärden.
Innan vi går in på det bör det påpekas att det inte är säkert att en
funktion f(x) har något gränsvärde när
![]() . I
sådana fall säger man att gränsvärdet inte existerar och symbolen
. I
sådana fall säger man att gränsvärdet inte existerar och symbolen
![]() är i så fall meningslös och bör då inte
användas. T.ex saknar
är i så fall meningslös och bör då inte
användas. T.ex saknar ![]() gränsvärde när
gränsvärde när
![]() i varje omgivning till 0 finns tal där funktionen antar värdet 1
liksom det finns tal där den antar värdet -1.
En funktion är (uppåt/nedåt) begränsad på en mängd om dess värdemängd där är
(uppåt/nedåt) begränsad. Om
i varje omgivning till 0 finns tal där funktionen antar värdet 1
liksom det finns tal där den antar värdet -1.
En funktion är (uppåt/nedåt) begränsad på en mängd om dess värdemängd där är
(uppåt/nedåt) begränsad. Om
![]() när
när
![]() är f(x) begränsad på en omgivning till a: till
är f(x) begränsad på en omgivning till a: till ![]() finns
en omgivning till a, så att A-1<f(x)<A+1, när x ligger i
omgivningen till a, men är
finns
en omgivning till a, så att A-1<f(x)<A+1, när x ligger i
omgivningen till a, men är ![]() . Man säger att f(x) är
begränsad i närheten av a. Eftersom 1/x inte är begränsad i någon
omgivning till 0, har 1/x inget gränsvärde när
. Man säger att f(x) är
begränsad i närheten av a. Eftersom 1/x inte är begränsad i någon
omgivning till 0, har 1/x inget gränsvärde när
![]() .
.
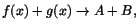 när
när
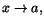
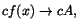 när
när
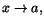
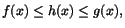 i en omgivning till a och A=B, så
har vi att
i en omgivning till a och A=B, så
har vi att
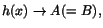 när
när
 .
.
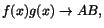 när
när
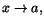
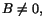 att
att
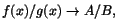 när
när
 .
.
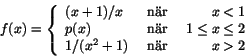
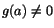 .
.
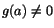 .
.
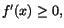 på ]a,b[, så är så är f växande på [a,b].
på ]a,b[, så är så är f växande på [a,b].