Parallellogrammens area är också längden av kryssprodukten
![]()
Svar: ![]() .
.
![]()
![]()
![]()
Svar: a=-1/2 och f'(0)=1/3.
- (a)
- Låt
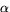 vara den vinkel som finns två gånger i den
likbenta triangeln och x vara längden på de båda lika långa
benen. Triangelns area är då
vara den vinkel som finns två gånger i den
likbenta triangeln och x vara längden på de båda lika långa
benen. Triangelns area är då
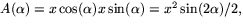 där
där
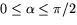 . Derivering ger
. Derivering ger
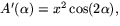 som är noll när
som är noll när 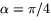 och negativt när
och negativt när 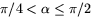 samt positivt när
samt positivt när 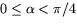 . Av detta följer att arean är störst när de båda
lika vinklarna i triangeln är
. Av detta följer att arean är störst när de båda
lika vinklarna i triangeln är 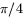 . Den återstående vinkeln är
då
. Den återstående vinkeln är
då 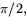 och triangeln är rätvinklig.
och triangeln är rätvinklig.
- (b)
- Vi låter x beteckna länden av de båda lika triangelbenen i
en gavel. Arean av sådan är då
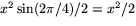 . Vi låter y beteckna tältets
längd. Volymen är då V=x2y/2 och takets area är 2xy, så att
materialåtgången blir M(x)=x2+2xy=x2+4V/x, där x>0.
. Vi låter y beteckna tältets
längd. Volymen är då V=x2y/2 och takets area är 2xy, så att
materialåtgången blir M(x)=x2+2xy=x2+4V/x, där x>0.
Derivering av M ger M'(x)=2x-4V/x2, som är noll när x=(2V)1/3. Derivatan är negativ när x är mindre än detta värde och positiv när x är större än det. Vi ser att M har ett minimum när x=(2V)1/3 och då är också y=(2V)1/3.
Svar: Tältet ska ha längd (2V)1/3 liksom katetrarna i gaveln.