Förslag till lösning av inlämningsuppgift 1
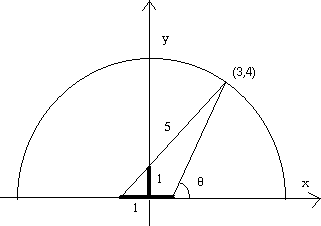
- Lägg in ett koordinatsystem som i figuren.
Vi får ingen upplysning av den aktuella sidan fram till
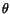 väljs
så att linjen genom de två punkterna (-1,0) och (0,1) också går
genom
väljs
så att linjen genom de två punkterna (-1,0) och (0,1) också går
genom
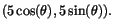 Linjen genom punkterna har
ekvationen y=x+1 och (halv)cirkeln har ekvationen
x2+y2=25. Detta ger
25=x2+(x+1)2=2x2+2x+1, som
har lösningarna x=3, (respektive x=-4). Den intressanta punkten
på cirkeln är alltså (3,4) som är
Linjen genom punkterna har
ekvationen y=x+1 och (halv)cirkeln har ekvationen
x2+y2=25. Detta ger
25=x2+(x+1)2=2x2+2x+1, som
har lösningarna x=3, (respektive x=-4). Den intressanta punkten
på cirkeln är alltså (3,4) som är
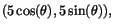 när
när
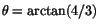 . Vi har alltså
. Vi har alltså 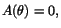 när
när
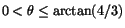 .
När vinkeln
.
När vinkeln 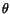 är
är 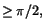 blir hela den aktuella sidan
upplyst och vi får
blir hela den aktuella sidan
upplyst och vi får 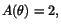 när
när
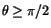 .
Linjen genom de två
punkterna
.
Linjen genom de två
punkterna
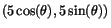 och (0,1) har
ekvationen
och (0,1) har
ekvationen
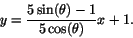
Linjen skär därför x-axeln i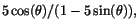 vilket betyder
att den upplysta bredden på sidan är
vilket betyder
att den upplysta bredden på sidan är
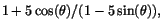 så
så
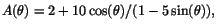 när
när
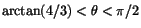 .
.
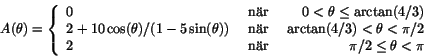
- Grafens utseende:
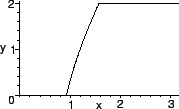
- Av uttrycken för
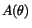 ser vi att det inte är något
problem med kontinuiteten utom möjligen i
ser vi att det inte är något
problem med kontinuiteten utom möjligen i 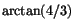 och
och
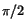 . (
. (
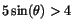 mellan dessa vinklar.)
När
mellan dessa vinklar.)
När
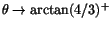 har vi att
har vi att
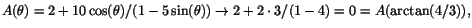 eftersom
eftersom
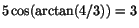 och
och
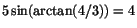 . När
. När
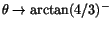 har vi att
har vi att
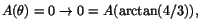 så vi har kontinuitet i
så vi har kontinuitet i
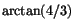 .
När
.
När
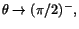 har vi att
har vi att
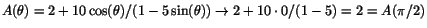 . När
. När
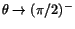 har vi att
har vi att
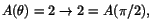 så vi har kontinuitet i
så vi har kontinuitet i
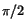 .
.
- Vi undersöker differenskvoten
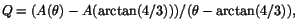 när
när
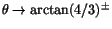 .
När
.
När
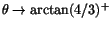 har vi
har vi

som är ett gränsvärde av typen ``0/0''. Enligt L'H har detta samma gränsvärde som
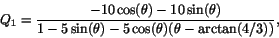
om gränsvärdet av Q1 existerar. Vi har
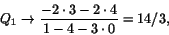
när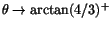 .
När
.
När
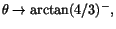 har vi däremot
har vi däremot
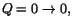 så Q har inget gränsvärde när
så Q har inget gränsvärde när
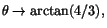 och därför är
och därför är 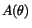 inte deriverbar i
inte deriverbar i 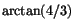 .
Vi undersöker differenskvoten
.
Vi undersöker differenskvoten
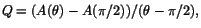 när
när
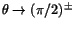 .
När
.
När
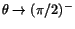 har vi
har vi
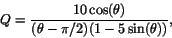
som är ett gränsvärde av typen ``0/0''. Enligt L'H har detta samma gränsvärde som
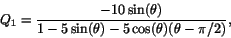
om gränsvärdet av Q1 existerar. Vi har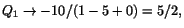 när
när
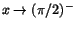 När
När
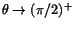 har vi
har vi
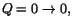 så
så 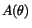 är inte deriverbar i
är inte deriverbar i 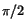
Svar: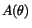 är kontinuerlig i alla punkter
är kontinuerlig i alla punkter
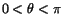 och deriverbar i alla punkter utom i
och deriverbar i alla punkter utom i 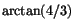 och
och 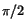 .
.
Jan-Alve Svensson
2002-09-25