Förslag till lösning av inlämningsuppgift 2
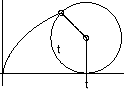
Navet befinner sig vid tiden t i (t,1).
I förhållande till denna
medelpunkt har den intressanta punkten koordinaterna
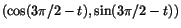 . Detta leder till parametriseringen . Detta leder till parametriseringen
Vi har
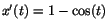 och och
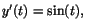 vilket ger vilket ger
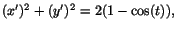 så så
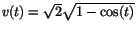 . Vi ser att största värdet av v(t)
är 2 och minsta värdet är 0.
Den vid tiden t tillryggalagda sträckan s(t) bestäms av . Vi ser att största värdet av v(t)
är 2 och minsta värdet är 0.
Den vid tiden t tillryggalagda sträckan s(t) bestäms av
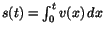 .
Vi beräknar en primitiv funktion till .
Vi beräknar en primitiv funktion till
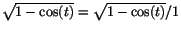 genom att först förlänga med genom att först förlänga med
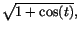 så vi får så vi får
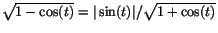 . Vi får se upp eftersom
vi delat med 0, när x är en udda heltalsmultipel av . Vi får se upp eftersom
vi delat med 0, när x är en udda heltalsmultipel av 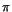 .
Vi har .
Vi har
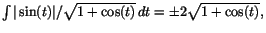 där
vi ska använda minustecken när där
vi ska använda minustecken när 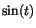 är <0 och plustecken när är <0 och plustecken när 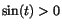 annars.
Vi får alltså
annars.
Vi får alltså
Vi undersöker om f(t) blir deriverbar i 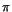 om vi sätter om vi sätter
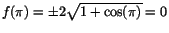 . Differenskvoten blir . Differenskvoten blir
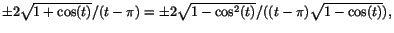 efter förlängning med efter förlängning med
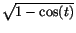 .
När .
När 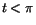 blir differenskvoten blir differenskvoten
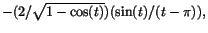 där den första faktorn har
gränsvärdet där den första faktorn har
gränsvärdet 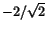 när när
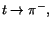 medan den andra
ger ett gränsvärde av typen ``0/0''. L'Hospitals regel ger oss
kvoten medan den andra
ger ett gränsvärde av typen ``0/0''. L'Hospitals regel ger oss
kvoten 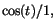 med gränsvärdet -1, när med gränsvärdet -1, när
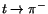 . Det betyder att differenskvoten har gränsvärdet . Det betyder att differenskvoten har gränsvärdet 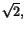 när
när
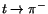 .
Även när .
Även när 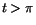 blir differenskvoten blir differenskvoten
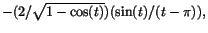 eftersom nu eftersom nu
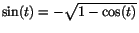 . Gränsvärdet av detta blir . Gränsvärdet av detta blir 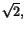 enligt samma räkningar som tidigare.
Vi får nu att
enligt samma räkningar som tidigare.
Vi får nu att
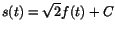 när när
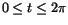 . Eftersom
0=s(0) och . Eftersom
0=s(0) och
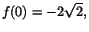 har vi C=4 och har vi C=4 och
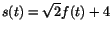 .
Vi ser att när hjulet rullat ett varv ( .
Vi ser att när hjulet rullat ett varv (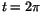 ) har punkten
tillryggalagt sträckan 8. Det betyder att vi har ) har punkten
tillryggalagt sträckan 8. Det betyder att vi har
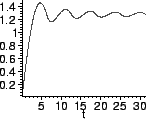
En skiss av grafen till medelhastigheten under tiden 0 till t,
s(t)/t, ser ut så här
Jan-Alve Svensson
2002-10-15
|