Lösning av TMA305 Envariabelanalys I, del a, 02 10 21
1. Fyrhörningen med hörn i origo, (0,1), P och (2,0) har arean
ab+a(1-b)/2+(2-a)b/2=a/2+b.
![\includegraphics [scale=1.5]{lsnTMA305a021021figA.eps}](img1.gif) |
![\includegraphics [scale=1.5]{lsnTMA305a021021figB.eps}](img2.gif) |
där A(b) är triangelns area när P har y-koordinaten b. Vi söker b så att A(b) är störst möjlig. Ett sådant värde på b är en kritisk punkt till A(b), vilket ger oss
Vi får
Svar:
2. Av formeln för funktionen ser vi att den är deriverbar utom möjligen i x=0. Differenskvoten där är
som ger ett gränsvärde av typ ``0/0'', när
där nämnaren går mot noll när
Av samma skäl som tidigare måste täljaren gå mot noll: 0=-4-2b, eller b=-2. Ytterligare användning av l'Hospitals regel ger
som har gränsvärdet 16/6=8/3, när
som vi ser är kontinuerlig ( när x>-1/2) utom möjligen i x=0. För att undersöka kontinuitet där ska vi undersöka gränsvärdet av
när
som ger gränsvärde av samma typ. Ytterligare användning av regeln ger
som ger gränsvärde av samma typ igen. Ytterligare användning av regeln ger
som har gränsvärdet 16/6=f'(0), när
Svar: a=2, b=-2, funktionen är definierad när x>-1/2 och derivatan är kontinuerlig.
3.
(a) Vi har med hjälp av trigonometriska ettan att6. Man har
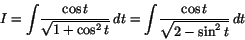
eller

vilket leder oss till variabelsubstitutionen. Vi får då
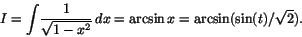
Svar:.
(b) Faktorisering av nämnaren som har nollstället 1/2, ger
2t3+3t2+2t-2=(2t-1)(t2+2t+2)
där faktorn av grad två saknar reella nollställen. Partialbråksuppdelning ger

Det första bråket har den primitiva funktionen. Det andra bråket skriv om:
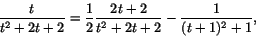
där det första bråket har den primitiva funktionen
och det andra
. Den ursprungliga rationella funktionen har därför den primitiva funktionen
F(t)=F1(t)-F2(t)+F3(t),
eller
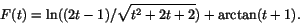
Eftersomnär
och
blir integralen i uppgiften konvergent med värdet
.
Svar: Integralen är konvergent med värdet
.
Svar:
7. Enligt kedjeregeln är (f(g(x)))'=f'(g(x))g'(x). Derivatan av den sammansatta funktionen är därför, när x=1, f'(g(1))g'(1)=f'(2)9=(1/3)9=3.
Svar: 3.
8. Partiell integration ger
Svar: (t2-2t+3)et.
9. Tangentlinjen går genom
Svar:
10. Skrivning på gemensamt bråkstreck ger uttrycket
Eftersom nämnaren går mot noll när
Svar: a=-2 och gränsvärdet blir 1/2.
11. Vi skriver om uttrycket som ska integreras:
där den första kvoten till höger har den primitiva funktionen
som har den primitiva funktionen
Svar: Integralen är konvergent med värdet
Jan-Alve Svensson
2002-10-21