Repetitionsuppgifter

Derivata och kontinuitet
 
1. Låt

$$f(x)=\left\{ \begin{array}{lcr} (e^{x}-1-x)/(xe^{x}-x) & ... ...neq 0\\ \alpha & \mbox{ när } & x=0. \end{array} \right.$$

Bestäm $\alpha$ så att f blir kontinuerlig i alla reella tal. Visa också att f blir deriverbar i x=0, för detta val av $\alpha$ och bestäm f'(0).
 
2. Visa att funktionen

$$f(x)=\left\{ \begin{array}{lcl} \sin(x)/x & \mbox{ när } & x\neq 0\\ 1 & \mbox{ när } & x=0, \end{array}\right.$$

är deriverbar i alla reella tal och bestäm f'(x). Visa också att f'(x) är kontinuerlig.
 
3. Bestäm ett polynom P(x), av lägsta möjliga grad, så att funktionen

$$f(x)=\left\{\begin{array}{lcl} \cos(x)& \mbox{ när } & x<0,... ...q 1,\\ 2+\ln(x^{2})& \mbox{ när }& 1<x, \end{array}\right.$$

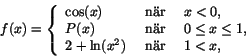
blir överallt deriverbar.
 
4. Bestäm konstanterana a, b och c, så att funktionen

$$f(x)=\left\{\begin{array}{lcl} a+bx+cx^{2}& \mbox{ när } ... ... \arctan(x)& \mbox{ när } &x\geq 1\\ \end{array}\right.$$

blir två gånger deriverbar.
 
5. Bestäm konstanten a så att funktionen

$$f(x)= \left\{ \begin{array}{lcl} -2+\ln(x+1)/x &\mbox{ när }& x\neq 0\\ a & \mbox{ när } & x=0, \end{array}\right.$$

som är definierad för x>-1, blir deriverbar över allt. Är derivatan kontinuerlig?
 
6. Bestäm konstanten a så att funktionen

$$f(x)= \left\{ \begin{array}{rl} (\ln(x+1)-x)/x^2 & \mbox... ...ch } x\neq 0 \\ a & \mbox{ när } x=0, \end{array} \right.$$

blir deriverbar i x=0. Bestäm också derivatan.
 
7. Bestäm konstanterna a och b så att funktionen

$$f(x)=\left\{ \begin{array}{lcr} (\sqrt{1+ax}-2x-1)/(x^{2... ...r } & x\neq 0\\ b & \mbox{ när }& x=0, \end{array}\right.$$

blir kontinuerlig.
 
Användning av derivata
 
8. Visa att

$$\mbox{e}^{x}>1+(1+x)\ln(1+x),$$

när x>0.
 
9. Bestäm de lokala extrempunkterna till funktionen

$$f(x)=\frac{x^{2}+x-2}{x+3}$$

Undersök också funktionen med avseend på konkavitet.
 
10. Man vill göra ett tält bestående av två gavlar och ett tak men inget golv. Gavlarna ska vara rätvinkliga likbenta trianglar med den räta vinkeln upp och tälet ska ha volym V. Hur ska tältet se ut om man vill minimera åtgången av tyg.
 
11. Man drar en tangentlinje till funktionen f(x)=e^-x i en punkt (a,f(a)), där a>0. Den skär x- och y-axeln i P respektive Q och man låter A vara arean av triangeln med hörn i dessa båda punkter samt origo. Har A ett största eller minsta värde? Vad är de i så fall?
 
12. Tangentlinjen till y=x² när x=1 är också tangentlinje till en cirkel med medelpunkt i (8,0). Bestäm ekvationen för denna cirkel.
 
13. Om den deriverbara funktionen f(x), definierad på ett intervall, vet man att varje punkt (x₀,f(x₀)) på kurvan y=f(x) har en normal som går genom (2x₀,0). Visa att kurva är del av en hyperbel, om f'(x) inte är konstant.
 
14. Man vill, om möjligt, bestämma en deriverbar funktion f(x) definierad för x>0, så följande villkor är uppfyllt: om man drar tangentlinjen i en punkt (x,f(x)) på grafen till funktionen, så ska denna skära y-axeln på avståndet $\sqrt{x^{2}+1}$ från (x,f(x)). Finns det någon sådan funktion? Bevisa ditt påstående! Integration
 
15. Beräkna

$$\mbox{a) }\int x\arctan(x)\,dx \mbox{\hspace{1 cm}}\mbox{b) }\int\frac{\cos(x)}{\sin^{3}(x)+1}\,dx$$

 
16. Beräkna

$$\mbox{a) }\int\frac{\sqrt{x}}{1+\sqrt{x}}\,dx \mbox{\hspace{1 cm}}\mbox{b) }\int\frac{\tan(x)}{\cos(x)+2}\,dx$$

 
17. Beräkna

$$\int_{0}^{\sqrt{2}-1}\frac{x}{\sqrt{1-2x-x^{2}}}\,dx,$$

om den är konvergent. Visa annars att den är divergent.
 
18. En partikels rörelse i planet beskrivs av den parametriserade kurvan $x(t)=\cos(t)/t,$ $y(t)=\sin(t)/t$. Beräkna den sträcka partikeln tillryggalägger mellan tiderna t=1 och t=2.
 
19. En partikels rörelse i planet beskrivs av den parametriserade kurvan $x(t)=(t/\sqrt{t^{2}+1})\cos(t),$ $y(t)=(t/\sqrt{t^{2}+1})\sin(t)$. Låt v(t) vara partikelns fart vid tiden t. Är

$$\int_{0}^{\infty}v(t)\,dt$$

konvergent eller divergent? Beräkna den i förekommande fall.
 
20. Bestäm en deriverbar funktion f(x), definierad för 0<x<1, som är strängt avtagande och sådan att tangentlinjen i varje punkt P på grafen till f(x) skär y-axeln i en punkt Q på avstånd 1 från P. Exempel på teoriuppgift 1
 
21. (a) Vad betyder det, enligt definitionen, att f(x) är deriverbar i x=a.
 
       (b) Visa, utgående från definitionen, att f(x)=x²+x-1 är deriverbar i x=1.
 
       (c)Visa att om funktionerna f(x) och g(x) är deriverbara i x=a, så är också f(x)g(x) deriverbar i x=a.
 
22. (a) Vad betyder det, enligt definitionen, att $f(x)\rightarrow A,$ när $x\rightarrow a$?
 
       (b) Visa, med definitionen, att $\sqrt{x}\rightarrow 1,$ när $x\rightarrow 1$.
 
       (c) Visa att om $f(x)\rightarrow A$ och $g(x)\rightarrow B,$ när $x\rightarrow a,$ så gäller att $f(x)g(x)\rightarrow B$.
 
23. (a) Vad menas med en över- respektive undersumma till en funktion f som är begränsad på ett intervall [a,b]? (Ge en matematisk definition.)
 
       (b) Hur lyder definitionen av att en funktion f, som är begränsad på [a,b], är integrerbar? Vad betyder i så fall $\int_{a}^{b}f(x)\,dx$?
 
       (c) Funktionen f(x) definieras som f(x)=2^x, när x är ett rationellt tal och f(x)=1 annars. Existerar $\int_{1}^{2}f(x)\,dx$? Motivera noggrant!
 
24. (a) Hur lyder den precisa matematiska definitionen av uttrycket $\lim_{x\rightarrow a}f(x)=A$?
 
       (b) Hur lyder den precisa matematiska definitionen av att funktionen f(x) är deriverbar i x=a?
 
       (c) Visa utgående från definitionen att funktionen f(x)=x³ är deriverbar i varje punkt.
 
Exempel på teoriuppgift 2
 
25. Formulera och bevisa medelvärdessatsen. Ge oclså exempel på en tillämpning av denna sats.
 
26. (a) Vad menas med en övre begränsning till en mängd av reella tal?
 
       (b) Formulera och bevisa Inkapslingssatsen.
 
       (c) I satsen används en speciell typ av intervall. Visa med ett exempel att satsen inte gäller för allmänna intervall.
 
27. Visa att en kontinuerlig funktion på intervallet [a,b] är begränsad.
 
28. Formulera och bevisa kedjeregeln för f(g(x)). Förslag till svar

1) a=1/2, f'(0)=-1/12    3) P(x)=x²+1    4) $(\pi-3)/4+x-x^{2}/4$    5) a=-1, ja 6) a=-1/2,

$$f'(x)=\left\{ \begin{array}{lcr} (x^{2}+2x-2(x+1)\ln(x+... ... }& x\neq 0\\ 1/3 & \mbox{ när } &x=0 \end{array}\right.$$

7) a=2, b=-1    9) $x=-5,\,-1,$ konkav uppåt när $x\geq -3,$ nedåt när $x\leq -3$
10) höjd=längd=(2V)^1/3    11) största värde 2/e, minsta värde saknas    12) (x-8)²+y²=45
14) T.ex. $f(x)=\ln(x)$    15 a) $(x^{2}+1)\arctan(x)/2+x/2$
15 b) $\ln(\sin(x)+1)/3-\ln(\sin^{2}(x)-\sin(x)+1)/6+\arctan(-1+2\sin(x)/\sqrt{3})/\sqrt{3}$
16 a) $x-2\sqrt{x}+2\ln(1+\sqrt{x})$    16 b) $(1/2)\ln(1+2/\cos(x))$
17) $1-\pi/4$    18) $-\sqrt{5}/2+\sqrt{2}+\ln(2+\sqrt{5})-\ln(1+\sqrt{2})$    18) divergent

19) $-\sqrt{1+x^{2}}+(1/2)\ln(-1+2/(1-\sqrt{1-x^{2}}))$