Tentamen i TMA 305 Envariabelanalys I, del A,
02 01 14, kl 8.45-11.45.
- 1.
- En partikel rör sig längs den räta linjen genom punkterna
(0,3,-2) och (1,5,0). Vad är det minsta avståndet mellan
partikeln och punkten (4,2,6)?
- 2.
- Bestäm konstanten a så att funktionen
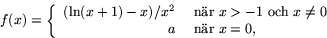
blir deriverbar i x=0. Bestäm också derivatan.
- 3.
- Man vill göra ett tält med utseende som i figuren och med given volym V.
- (a)
- Visa att en likbent triangel har störst area när den
är rätvinklig.
- (b)
- Hur ska tältet se ut om man vill att gavlarna ska vara
rätvinkliga likbenta trianglar och att materialåtgången ska vara
minst möjlig? Tältet ska sakna golv.
- 4.
- (a)
- Hur lyder den precisa matematiska definitionen av uttrycket
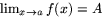 ?
?
- (b)
- Hur lyder den precisa matematiska definitionen av att
funktionen f(x) är deriverbar i x=a?
- (c)
- Visa utgående från definitionen att funktionen f(x)=x3 är
deriverbar i varje punkt.
- 5.
- Visa att en kontinuerlig funktion på intervallet [a,b] är
begränsad.
Efter skrivningstidens slut finns förslag till lösningar på kursens
webbsida:
http://www.math.chalmers.se/Math/Grundutb/CTH/tma305a/0102/
JAS
![]()
![\includegraphics [scale=.5]{talttak.eps}](img4.gif)
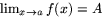 ?
?