$\parbox{6cm}{MATEMATIK \\ Chalmers tekniska högskola\\ \\ Skriv nam... ...nnummer på varje inlämnat papper och linje samt inskrivningsår på omslaget\\ }$

$\parbox{6cm}{Hjälpmedel: typgodkänd räknare\\ Tele: Milena Anguelova \\ 0740-45 90 22\\ }$

Tentamen i TMA 305 Envariabelanalys I, del A, 02 08 19, kl 14.15-18.15.

1.

Motivera att funktionen

$$f(x)=x^{2}/2-3x/2+\arctan(x)$$

har ett minsta värde och bestäm detta.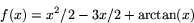

2.

Bestäm konstanten a så att funktionen

$$f(x)=\left\{ \begin{array} {rcl} (e^{2x}-1-2x)/x^{2} &\mbox{ när }& x\neq 0\\ a &\mbox{ när }& x=0 \end{array}\right.$$

blir deriverbar över allt. Avgör också om f'(x) är kontinuerlig.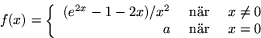

3.

Cirklarna x²+y²=1 och (x-2)²+y²=4 har en gemensam tangent med positiv riktningskoefficient. Bestäm ekvationen för denna linje.

4.

(a)

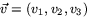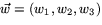Hur definieras kryssprodukten av vektorerna $\vec{v}=(v_{1},v_{2},v_{3})$ och $\vec{w}=(w_{1},w_{2},w_{3})$ algebraiskt? Svara utan determinant.

(b)

visa att 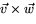$\vec{v}\times\vec{w}$ är vinkelrät mot 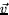$\vec{v}$. Använd den algebraiska definitionen av kryssprodukten.

(c)

Bestäm en normal till planet genom de tre punkterna (1,2,3), (2,1,3) och (1,0,1).

5.

Formulera och bevisa kedjeregeln för f(g(x)).

Förslag till lösningar kommer att finnas på kursens webbsida från tisdagen den 20 augusti:

http://www.math.chalmers.se/Math/Grundutb/CTH/tma305a/0102/

VÄND!

Under kursens gång har det förekommit löpande examination. Den maximala poängen från denna är 18. Om Du vill komplettera Din poäng från detta moment kan Du lösa uppgifter nedan. Inom parentes vilka uppgifter som är aktuella för Dig. T.ex. anger (< 12) att uppgiften gäller Dig vars poäng från den löpande examinationen är < 12. Bara korrekt valda uppgifter kommer att beaktas!

Varje uppgift kan ge tre poäng. Fullständiga lösningar krävs för poäng!

6.

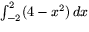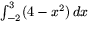(<3) Vilket av talen $\int_{-2}^{2}(4-x^{2})\,dx$ och $\int_{-2}^{3}(4-x^{2})\,dx$ är störst. Motivera noggrant!

7.

(<6) Man vet att f(2)=4, f'(2)=-1/5 och att f är inverterbar. Vad är derivatan till f^-1(x) i x=4?

8.

(<9) Man vet att f'(3)=4, g(2)=3 och att g'(2)=1/2. Vad är då derivatan till f(g(x)) i x=2?

9.

(<12) Bestäm en ekvation för planet genom de tre punkterna (1,2,3), (2,1,3) och (1,0,1).

10.

(<15) Bestäm den linjära approximationen till 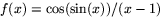$f(x)=\cos(\sin(x))/(x-1)$ i punkten x=0.

11.

(<18) Bestäm ett polynom p av grad tre med följande egenskaper:

(a)

derivatan är negativ mellan 1 och 3 men positiv för övrigt,

(b)

p(-1)=1.

JAS